✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
(Fuvest, 2018) Considere a função real definida por [tex]f(x)= \sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}-x[/tex].
a) Qual é o domínio de [tex]f[/tex]?
b) Encontre o(s) valor(es) de [tex]x[/tex] para o(s) qual(is) [tex]f(x) = 0[/tex].
Solução 1
a) Para que as duas raízes quadradas que aparecem na expressão de [tex]f[/tex] definam números reais, devemos ter [tex]x-\dfrac{1}{x} \geq 0~[/tex] e [tex]~1-\dfrac{1}{x}\geq 0[/tex].
Vamos reescrever adequadamente essas duas condições; assim, obtemos o sistema [tex]S[/tex]:
[tex]\qquad S: \begin{cases}x-\dfrac{1}{x} \geq 0\\
1-\dfrac{1}{x}\geq 0 \end{cases}~;\\
~~\\
\qquad S: \begin{cases}\dfrac{x^2-1}{x} \geq 0\\
\dfrac{x-1}{x}\geq 0
\end{cases}~;\\
~~\\
\qquad S: \begin{cases}(x+1)\dfrac{x-1}{x} \geq 0\\
\dfrac{x-1}{x}\geq 0
\end{cases}~.\\
~~[/tex]
Da segunda inequação da última forma de [tex]S[/tex], temos duas possibilidades:
[tex]\qquad \dfrac{x-1}{x} = 0~~[/tex] ou [tex]~~\dfrac{x-1}{x} \gt 0[/tex].
- Caso seja [tex]\dfrac{x-1}{x} = 0[/tex], então teremos [tex]x = 1[/tex] e, com isso, [tex]x+1=2\gt 0[/tex]. Assim, [tex]\boxed{x+1\gt 0}\,.[/tex]
- Por outro lado, se tivermos [tex]\dfrac{x-1}{x} \gt 0[/tex], então [tex]x+1\geq 0[/tex], pois, caso contrário (se [tex]x+1\lt 0[/tex]), então teríamos [tex](x+1)\dfrac{x-1}{x} \lt 0[/tex], o que contradiz a primeira inequação do último sistema. Logo, [tex]\boxed{x+1\geq 0_{_{~}}}\,.[/tex]
Assim, podemos reescrever o sistema [tex] S[/tex] como:
[tex]\qquad S:\begin{cases} \dfrac{x-1}{x}\geq 0\\x+1\geq 0
\end{cases}.\\
~~[/tex]
Observe que [tex]0[/tex] não pertence ao domínio de [tex]f[/tex], pois se colocássemos [tex]x=0[/tex] na expressão de [tex]f[/tex], teríamos uma divisão por [tex]0[/tex], o que não pode acontecer. Portanto, [tex]x\neq 0[/tex].
E, sendo [tex]x\neq 0[/tex], temos [tex]x^2\gt 0[/tex]; assim, podemos multiplicar a primeira inequação do sistema [tex] S[/tex] por [tex]x^2[/tex], obtendo
[tex]\qquad S:\begin{cases} \dfrac{x-1}{x}\geq 0\\x+1\geq 0
\end{cases}\\
~~\\
\qquad S:\begin{cases} x(x-1)\geq 0\\x\geq -1
\end{cases}.[/tex]
Agora vamos fazer um estudo de sinais das inequações que aparecem na última forma do sistema [tex] S[/tex].
Considerando a função [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x)=x(x-1)[/tex], os zeros dessa função são tais que
[tex]\qquad g(x)=0\\
\qquad x(x-1)=0\\
\qquad \boxed{x=0} ~\text{ ou } ~\boxed{x=1}.[/tex]
Observe, ainda, que o gráfico da função [tex]g[/tex] é uma parábola com a concavidade voltada para cima; assim, o conjunto solução da inequação [tex]x(x-1)\geq 0[/tex] é:
[tex]\qquad \boxed{C_1 = \{x\in\mathbb{R}\;|\; x\leq 0 \;\text{ou}\; x\geq 1\}}[/tex].
E, como já podemos perceber, o conjunto solução da inequação [tex]x\geq -1[/tex] é:
[tex]\quad \boxed{C_2 = \{x\in\mathbb{R}\;|\;x\geq -1\}}[/tex].
Logo, a solução do sistema [tex]S[/tex] é dada por [tex]C_1\cap C_2 = \{x\in\mathbb{R}\;|\; -1\leq x\leq 0 \;\text{ou}\; x\geq 1\}[/tex].
Finalmente, como já vimos que [tex]0[/tex] não pertence ao domínio de [tex]f[/tex], então
[tex]\quad D_f = \{x\in\mathbb{R}\;|\; -1\leq x\lt 0 \;\text{ou}\; x\geq 1\}[/tex]
ou ainda
[tex]\quad \fcolorbox{black}{#eee0e5}{$D_f = [-1,0[ \;\cup\; [1,+\infty [$}\,.[/tex]
b) Vamos denotar [tex]\sqrt{x-\dfrac{1}{x}}~[/tex] por [tex]~a~[/tex] e [tex]~\sqrt{1-\dfrac{1}{x}}[/tex] por [tex]~b[/tex], logo temos que [tex]f(x)=a+b-x[/tex].
Vamos determinar os valores de [tex]x[/tex] tais que [tex]f(x) = 0[/tex]; ou seja, vamos determinar os valores de [tex]x[/tex] para os quais [tex]\boxed{a+b=x}[/tex]
Vamos lá!
Note que, como [tex]a,b\geq 0[/tex], então [tex]x\geq 0[/tex]. Mas como [tex]a+b = x[/tex] e no item anterior vimos que [tex]x\neq 0[/tex], então [tex]a+b\neq 0[/tex].
Agora, observe que:
[tex]\qquad \begin{align}(a+b)(a-b) &= a^2-b^2 \\
&= \left(\sqrt{x-\dfrac{1}{x}}\right)^2-\left(\sqrt{1-\dfrac{1}{x}}\right)^2 \\
&= \left(x-\dfrac{1}{x}\right)-\left(1-\dfrac{1}{x}\right) \\
&= x-1,\end{align}[/tex]
donde concluímos que
[tex]\qquad a-b=\dfrac{x-1}{a+b}\\
\qquad \boxed{a-b=\dfrac{x-1}{x}}.[/tex]
Dessa forma, obtemos o seguinte sistema:
[tex]\qquad \begin{cases}a+b = x\\
a-b = \dfrac{x-1}{x}.\end{cases}[/tex]
Subtraindo a segunda equação da primeira, segue que
[tex]\qquad 2b= x-\dfrac{x-1}{x}\\
\qquad b=\dfrac{x^2-x+1}{2x}.[/tex]
Mas, por outro lado, [tex]b = \sqrt{1-\dfrac{1}{x}}[/tex]; portanto:
[tex]\qquad \sqrt{1-\dfrac{1}{x}} = \dfrac{x^2-x+1}{2x}[/tex]
[tex]\qquad 2x\sqrt{1-\dfrac{1}{x}} = x^2-x+1[/tex]
[tex]\qquad 2x\sqrt{\dfrac{x-1}{x}} = x^2-x+1[/tex]
[tex]\qquad 2\sqrt{x^2\cdot \dfrac{x-1}{x}} = x^2-x+1[/tex]
[tex]\qquad 2\sqrt{x^2-x} = x^2-x+1.\qquad \textcolor{#800000}{(i)}[/tex]
Agora, para simplificar as contas, vamos fazer [tex]\boxed{\textcolor{red}{\sqrt{x^2-x}=y}}[/tex]. Então, segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad 2\sqrt{x^2-x} = x^2-x+1\\
\qquad 2\textcolor{red}{\sqrt{x^2-x}}=\left(\textcolor{red}{\sqrt{x^2-x}}\right)^2+1\\
\qquad 2\textcolor{red}{y} = \textcolor{red}{y}^2+1\\
\qquad y^2-2y+1 = 0\\
\qquad \left(y-1\right)^2 = 0\\
\qquad y-1= 0\\
\qquad \textcolor{red}{y} = 1\\
\qquad \textcolor{red}{\sqrt{x^2-x}} = 1\\
\qquad \left(\sqrt{x^2-x}\right)^2 = 1^2\\
\qquad x^2-x = 1\\
\qquad x^2-x-1 = 0.[/tex]
Aplicando a fórmula resolutiva para equações do segundo grau para a equação [tex]x^2-x-1 = 0[/tex], encontramos [tex]x= \dfrac{1\pm\sqrt{5}}{2}.[/tex]
Mas, como vimos no início da solução, [tex]x\geq 0[/tex]; então, [tex]\boxed{x=\dfrac{1+\sqrt{5}}{2}}.[/tex]
Para finalizar, precisamos verificar se [tex]\dfrac{1+\sqrt{5}}{2}[/tex] é, de fato, um valor para o qual [tex]f(x)=0[/tex].
Para isso, note que, se [tex]x=\dfrac{1+\sqrt{5}}{2}[/tex], segue que:
[tex]\qquad x= \dfrac{1+\sqrt{5}}{2}\\
\qquad x^2=\left(\dfrac{1+\sqrt{5}}{2}\right)^2\\
\qquad x^2=\dfrac{1+2\sqrt{5}+5}{4}\\
\qquad x^2=\dfrac{2+2\sqrt{5}+4}{4}\\
\qquad x^2=\dfrac{2+2\sqrt{5}}{4}+\dfrac{4}{4}\\
\qquad x^2=\dfrac{1+\sqrt{5}}{2}+1\\
\qquad x^2=x+1.\qquad \textcolor{#800000}{(ii)}[/tex]
A partir da equação [tex]\textcolor{#800000}{(ii)}[/tex] e lembrando que [tex]\dfrac{1+\sqrt{5}}{2}\gt 0[/tex], segue que:
|
[tex]\qquad x^2=x+1\\ \qquad x^2-1=x\\ \qquad \dfrac{x^2-1}{x}=1\\ \qquad x-\dfrac{1}{x}=1\\ \qquad \sqrt{x-\dfrac{1}{x}}=\sqrt{1}\\ \qquad \sqrt{x-\dfrac{1}{x}}=1.[/tex] Como [tex]\sqrt{x-\dfrac{1}{x}}=a[/tex], temos que [tex]a=1.[/tex] |
[tex]\qquad x^2=x+1\\ \qquad 1=\dfrac{1}{x}+\dfrac{1}{x^2}\\ \qquad 1-\dfrac{1}{x}=\dfrac{1}{x^2}\\ \qquad \sqrt{1-\dfrac{1}{x}}=\sqrt{\dfrac{1}{x^2}}\\ \qquad \sqrt{1-\dfrac{1}{x}}=\dfrac{1}{x}\\ [/tex] Como [tex]\sqrt{1-\dfrac{1}{x}}=b[/tex], temos que [tex]b=\dfrac{1}{x}.[/tex] |
Daí, temos que
[tex]\qquad a+b= 1+\dfrac{1}{x}= \dfrac{x+1}{x} = \dfrac{x^2}{x} = x[/tex],
ou ainda
[tex]\qquad a+b-x=0.[/tex]
Portanto, [tex]f\left(\dfrac{1+\sqrt{5}}{2}\right)=f(x)=0[/tex], como queríamos.
Por tudo o que foi exposto, o único valor de [tex]x[/tex] para o qual [tex]f(x)=0[/tex] é [tex]~\fcolorbox{black}{#eee0e5}{$x = \dfrac{1+\sqrt{5}}{2}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
a) Vamos determinar a condição de existência da função [tex]f[/tex] em [tex]\mathbb{R}[/tex].
Para isso, devemos analisar a condição de existência das parcelas [tex]~\sqrt{x-\dfrac{1}{x}}~[/tex] e [tex]~\sqrt{1-\dfrac{1}{x}}[/tex], já que a expressão [tex]-x[/tex] é definida para qualquer número real. Mas perceba que nessas duas parcelas aparece a expressão [tex]\dfrac{1}{x}[/tex]; portanto devemos também analisar a existência dessa expressão em [tex]\mathbb{R}.[/tex]
Assim, vamos analisar a existência de três expressões numéricas no conjunto dos números reais:
[tex]\quad \quad \boxed{\dfrac{1}{x}}\quad[/tex] ; [tex]\quad \boxed{\sqrt{x-\dfrac{1}{x}}}\quad [/tex] ; [tex]\quad\boxed{\sqrt{1-\dfrac{1}{x}}}\,.[/tex]
- Inicialmente, perceba que para que a expressão [tex]\dfrac{1}{x}[/tex] defina um número real, basta que tenhamos [tex]x\ne 0[/tex].
Assim, esta é a nossa primeira condição de existência: [tex]\textcolor{blue}{C_1=]-\infty\,,0\,[\, \cup \, ]\, 0\, ,\, +\infty\,[}[/tex] - Agora, observe que para que a raiz quadrada [tex]~\sqrt{x-\dfrac{1}{x}}~[/tex] defina um número real, devemos ter [tex]~x-\dfrac{1}{x} \geqslant 0~[/tex].
Vamos, então, fazer a variação de sinal da expressão [tex]x-\dfrac{1}{x} ~[/tex]; mas antes, observe que:
[tex]\qquad\qquad x-\dfrac{1}{x} =\dfrac{x^2-1}{x} \,.[/tex]
Assim, podemos determinar a variação de sinal da expressão [tex]x-\dfrac{1}{x} ~[/tex] fazendo o estudo de variação de sinal da expressão [tex]\dfrac{x^2-1}{x}[/tex] e para isso, vamos estudar a variação de sinal do numerador e do denominador da fração.
Em um plano cartesiano [tex]xOy[/tex], o gráfico de [tex]y=x^2-1[/tex] é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar esse gráfico e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]x^2-1=0[/tex]; observe:
[tex]\qquad x^2-1=0\\
\qquad x^2=1\\
\qquad x_1=1 \qquad \text{e}\qquad x_2=-1\,. [/tex]Veja um esboço da parábola:
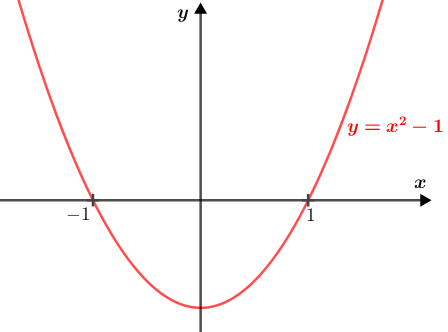
e a variação de sinal da expressão [tex]x-\dfrac{1}{x} ~[/tex], ou seja, os valores de [tex]x[/tex] para os quais a expressão define um número positivo, um número negativo ou o número [tex]0[/tex]:

Para a variação de sinal do denominador não é necessária nenhuma complicação, já que a expressão que define o denominador é [tex]x[/tex]:
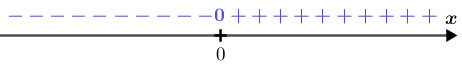
Lembrando das regrinhas de sinal para produtos e divisões:- produto/quociente de números com sinais contrários é um número negativo;
- produto/quociente de números com mesmo sinal é um número positivo.
e que não existe divisão por zero, podemos obter a variação de sinal da expressão [tex]\dfrac{x^2-1}{x}[/tex].
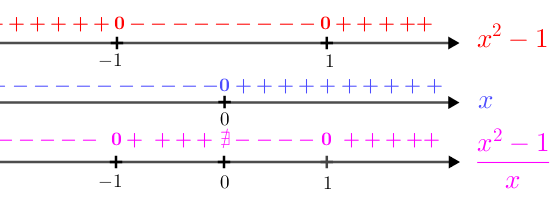
Portanto, a raiz quadrada [tex]~\sqrt{x-\dfrac{1}{x}}~[/tex] define um número real para valores de [tex]x[/tex] que estejam no conjunto [tex]\textcolor{#FF00FF}{C_2}[/tex] assim definido:
[tex]\qquad \textcolor{#FF00FF}{C_2=[\,-1\,,\,0\,[\,\cup\, [\,1\,,\,+\infty\, [}[/tex]. - Para que a raiz quadrada [tex]~\sqrt{1-\dfrac{1}{x}}~[/tex] defina um número real, devemos ter [tex]~1-\dfrac{1}{x} \geqslant 0~[/tex].
Vamos, agora, fazer a variação de sinal da expressão [tex]1-\dfrac{1}{x} ~[/tex]; mas antes, observe que:
[tex]\qquad\qquad 1-\dfrac{1}{x} =\dfrac{x-1}{x} \,.[/tex]
Assim, vamos determinar a variação de sinal da expressão [tex]1-\dfrac{1}{x} ~[/tex] fazendo o estudo de variação de sinal da expressão [tex]\dfrac{x-1}{x}[/tex]. Vamos, então, estudar a variação de sinal do numerador e do denominador dessa última fração.
Para o numerador não vamos precisar de gráficos; é só fazer continhas, e para o denominador já conhecemos a variação de sinal.[tex]~~\\
~~\\
\quad x-1 \gt 0 \iff x\gt 1 \quad[/tex]
[tex]\quad x-1 \lt 0 \iff x\lt 1 \quad[/tex]
[tex]\quad x-1 = 0 \iff x = 1\quad [/tex]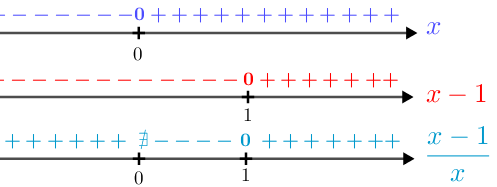
Dessa forma, para que a raiz quadrada [tex]~\sqrt{1-\dfrac{1}{x}}~[/tex] defina um número real os valores de [tex]x[/tex] devem estar no conjunto [tex]\textcolor{#0099CC}{C_3}[/tex] assim definido:
[tex]\qquad \textcolor{#0099CC}{C_3=[\,-\infty\,,\,0\,[\,\cup\, [\,1\,,\,+\infty\, [}[/tex].
Podemos finalizar este item, analisando para quais valores de [tex]x[/tex] as três restrições são simultaneamente satisfeitas, Para isso, faremos a interseção entre [tex]\textcolor{blue}{C_1}[/tex], [tex]\textcolor{#FF00FF}{C_2}[/tex] e [tex]\textcolor{#0099CC}{C_3}[/tex]:
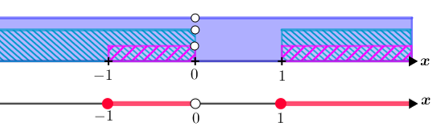
Perceba que as três condições são satisfeitas simultaneamente para todos os valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#FFBBC9}{$ -1\leqslant x \lt0$}[/tex] ou [tex]\, \fcolorbox{black}{#FFBBC9}{$ x\geqslant 1$}\,[/tex] e, portanto, [tex]\quad \fcolorbox{black}{#eee0e5}{$D_f=\ [-1,0[ \;\cup\; [1,+\infty [$}\,.[/tex]
b) Neste item vamos determinar o(s) valor(es) de [tex]x[/tex] para o(s) qual(is) [tex]f(x) = 0[/tex], ou seja, [tex]\sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}-x=0[/tex].
Antes de mais nada, observe que se [tex]f(x) = 0[/tex], então [tex]\sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}=x[/tex].
Sabemos que raízes quadradas são números maiores ou iguais a zero; dessa forma, temos que [tex]\sqrt{x-\dfrac{1}{x}} \geqslant 0[/tex] e [tex]\sqrt{1-\dfrac{1}{x}} \geqslant 0[/tex], donde [tex]\sqrt{x-\dfrac{1}{x}} + \sqrt{1-\dfrac{1}{x}} \geqslant 0[/tex] e, portanto, [tex]x \geqslant 0.[/tex] Mas sabemos que [tex]x\ne 0[/tex], logo [tex]x \gt0.[/tex]
Agora vamos fazer muitas contas….
Se [tex]\sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}-x=0[/tex], então [tex]\sqrt{x-\dfrac{1}{x}}=x-\sqrt{1-\dfrac{1}{x}}.[/tex]
Elevando ambos os membros dessa igualdade ao quadrado, segue que:
[tex]\quad \left(\sqrt{x-\dfrac{1}{x}}\right)^2=\left(x-\sqrt{1-\dfrac{1}{x}}\right)^2[/tex]
[tex]\quad x-\dfrac{1}{x}=x^2-2x\sqrt{1-\dfrac{1}{x}}+\left(1-\dfrac{1}{x}\right)[/tex]
[tex]\quad x=x^2-2x\,\sqrt{1-\dfrac{1}{x}}+1[/tex]
[tex]\quad 2x\, \sqrt{1-\dfrac{1}{x}}=x^2+1-x[/tex].
Elevando ambos os membros dessa última igualdade ao quadrado, segue agora que
[tex]\quad \left(2x\sqrt{1-\dfrac{1}{x}}\right)^2= \left(x^2+1-x\right)^2[/tex]
[tex]\quad 4x^2\,\left(1-\dfrac{1}{x}\right)= x^4+x^2+1-2x^3+2x^2-2x[/tex]
[tex]\quad 4x^2-4x= x^4+x^2+1-2x^3+2x^2-2x[/tex]
[tex]\quad x^4-2x^3-x^2+2x+1=0[/tex].
Como [tex]x \ne 0[/tex], podemos dividir a última igualdade por [tex]x^2[/tex] e, com isso, teremos:
[tex]\quad x^2-2x-1+\dfrac{2}{x}+\dfrac{1}{x^2}=0\\
\quad x^2+\dfrac{1}{x^2}-2\left(x-\dfrac{1}{x}\right)-1=0.\qquad \textcolor{#800000}{(i)}[/tex]
Agora, vamos fazer uma mudança de variável:
[tex]\qquad m=x-\dfrac{1}{x}. \qquad \textcolor{#800000}{(ii)}[/tex]
Com isso:
[tex]\qquad m^2=\left(x-\dfrac{1}{x}\right)^2\\
\qquad m^2=x^2-2\cdot x \cdot \dfrac{1}{x}+ \left(\dfrac{1}{x}\right)^2\\
\qquad m^2=x^2-2+\dfrac{1}{x^2}\\
\qquad m^2+2=x^2+\dfrac{1}{x^2}.\qquad \textcolor{#800000}{(iii)}[/tex]
Substituindo [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex] em [tex]\textcolor{#800000}{(i)}[/tex], vem que:
[tex]\qquad m^2+2-2m-1=0[/tex]
[tex]\qquad m^2-2m+1=0[/tex]
[tex]\qquad \left(m-1\right)^2=0[/tex].
Com isso, [tex]m-1=0[/tex], ou seja, [tex]m=1[/tex]. Então, por [tex]\textcolor{#800000}{(ii)}[/tex] obtemos que [tex]x-\dfrac{1}{x}=1[/tex] e, dessa forma, segue que:
[tex]\qquad x-\dfrac{1}{x}=1\\
\qquad x^2-1=x\\
\qquad x^2-x-1=0.[/tex]
Veja que o valor de [tex]x[/tex] que estamos procurando é raiz dessa última equação, logo:
[tex]\qquad x=\dfrac{1 \pm \sqrt{1+4}}{2}=\dfrac{1 \pm \sqrt{5}}{2}[/tex]
[tex]\qquad x_1=\dfrac{1 + \sqrt{5}}{2}\quad [/tex] ou [tex]\quad x_2=\dfrac{1 – \sqrt{5}}{2}[/tex].
Como [tex]x \gt 0[/tex], concluímos que [tex]\boxed{x = \dfrac{1+\sqrt{5}}{2}}\,.[/tex]
Resta agora mostrar que, de fato, [tex]f\left( \dfrac{1+\sqrt{5}}{2}\right)=0.[/tex] Vamos lá
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\sqrt{\dfrac{1+\sqrt{5}}{2}-\dfrac{1}{\dfrac{1+\sqrt{5}}{2}}}+\sqrt{1-\dfrac{1}{\dfrac{1+\sqrt{5}}{2}}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\sqrt{\dfrac{1+\sqrt{5}}{2}-\dfrac{2}{1+\sqrt{5}}}+\sqrt{\dfrac{\dfrac{1+\sqrt{5}}{2}-1}{\dfrac{1+\sqrt{5}}{2}}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\sqrt{\dfrac{1+2\sqrt{5}+5-4}{2\left(1+\sqrt{5}\right)}}+\sqrt{\dfrac{\dfrac{1+\sqrt{5}-2}{2}}{\dfrac{1+\sqrt{5}}{2}}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\sqrt{\dfrac{2+2\sqrt{5}}{2+2\sqrt{5}}}+\sqrt{\dfrac{\sqrt{5}-1}{\sqrt{5}+1}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\sqrt{\dfrac{\sqrt{5}-1}{\sqrt{5}+1}\cdot\dfrac{\sqrt{5}-1}{\sqrt{5}-1}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\sqrt{\dfrac{5-2\sqrt{5}+1}{5-1}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\sqrt{\dfrac{6-2\sqrt{5}}{4}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\sqrt{\dfrac{\left(1-\sqrt{5}\right)^2}{4}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\dfrac{\sqrt{\left(1-\sqrt{5}\right)^2}}{\sqrt{4}}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\dfrac{|1-\sqrt{5}|}{2}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=1+\dfrac{\sqrt{5}-1}{2}-\dfrac{1+\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\dfrac{2+\sqrt{5}-1-1-\sqrt{5}}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=\dfrac{0}{2}[/tex]
[tex]\quad f\left(\dfrac{1+\sqrt{5}}{2}\right)=0.[/tex]
F I N A L M E N T E, podemos garantir que o único número real [tex]x[/tex] tal que [tex]f(x)=0[/tex] é [tex]\,\fcolorbox{black}{#eee0e5}{$x = \dfrac{1+\sqrt{5}}{2}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
