Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 8º ano do E. F.)
Encontre o horário exato mostrado no relógio abaixo.
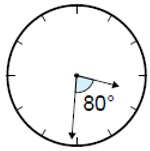
Solução
Como um relógio é dividido em doze partes iguais, concluímos que entre duas marcações sucessivas para horas temos um ângulo de [tex]\dfrac{360^\circ}{12}=30^\circ [/tex].
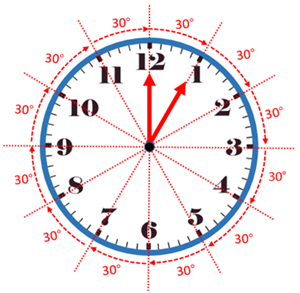
Na imagem do enunciado, percebemos que o ponteiro da hora está entre a terceira e a quarta marcações; então, isso significa que o relógio está marcando [tex]3[/tex] horas (ou [tex]15[/tex] horas) e alguns minutos.
Para encontrar os minutos, precisamos calcular os deslocamentos angulares de cada ponteiro após às [tex]3:00[/tex].
- Perceba que o ponteiro que indica os minutos completa uma volta ([tex]360^\circ[/tex]) a cada [tex]60[/tex] minutos, ou seja, ele se desloca [tex]6^\circ[/tex] a cada minuto. Se chamarmos de [tex]t[/tex] o tempo, em minutos, transcorrido após às [tex]3:00[/tex], o deslocamento angular do ponteiro foi de [tex]6^\circ \cdot t[/tex].
- Já o ponteiro que indica a hora, a cada [tex]60[/tex] minutos se desloca [tex]30^\circ[/tex]; logo, ele percorre [tex]0,5^\circ[/tex] por minuto. Em [tex]t[/tex] minutos, seu deslocamento será de [tex]0,5^\circ \cdot t[/tex].
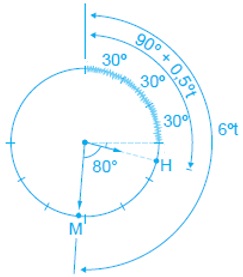
Note nessa última imagem que o deslocamento angular do ponteiro que indica os minutos é igual a “três divisões do relógio mais o deslocamento angular do ponteiro da hora mais o ângulo de [tex]80^\circ[/tex] entre os ponteiros”.
Assim:
[tex]\qquad 6^\circ \cdot t = 90^\circ + 0,5^\circ \cdot t +80^\circ[/tex]
[tex]\qquad 5,5^\circ \cdot t=170^\circ[/tex]
[tex]\qquad t=\dfrac{170^\circ}{5,5^\circ}[/tex]
[tex]\qquad t=\dfrac{340}{11}[/tex] minutos.
Portanto, o horário marcado pelo relógio é [tex]3[/tex] horas e [tex]\dfrac{340}{11}[/tex] minutos (aproximadamente [tex]3[/tex] horas, [tex]30[/tex] minutos e [tex]54[/tex] segundos).
Solução elaborada pelos Moderadores do Blog.
