Nesta Sala vamos explorar informalmente algumas das relações de volume.
Nas nossas ações, vocês vão encontrar outro sólido bastante presente no nosso cotidiano: o cone.
Esse objeto espacial, que lembra uma casquinha de sorvete, tem seu nome ligado a objetos de sinalização utilizados como demarcadores no trânsito das estradas e vias públicas.
 Imagem extraída de Freepik.
Imagem extraída de Freepik.
Diferentemente dos prismas e cilindros, os cones não têm duas bases paralelas, mas cones também podem ser retos ou oblíquos.
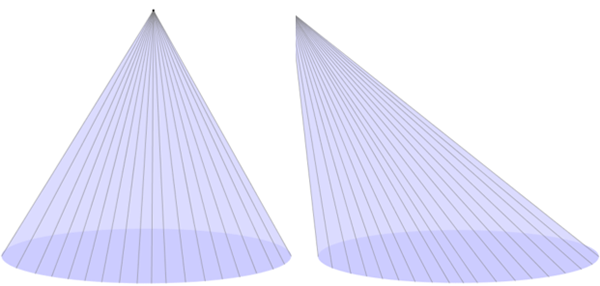
Atividade 17 – Explorando mais volumes
(a) Considerem os dois cilindros com raios 1 e 3 que aparecem na janela do aplicativo abaixo.
Ajustem a altura para que esses dois cilindros tenham o mesmo volume.
(1) Esperem o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar um dos pontos verdes, cliquem sobre ele com qualquer botão do mouse, mantenham o mouse pressionado e façam o movimento. (Se vocês estiverem utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se vocês estiverem usando um computador, vocês também poderão fazer os movimentos dos pontos verdes utilizando os seus teclados. Para isso, cliquem no ponto com o botão esquerdo do mouse e façam os movimentos utilizando as teclas “PgUp” ou “PgDn”. (Para movimentos “mais finos”, mantenham a tecla Shift do teclado apertada enquanto vocês fazem o movimento.)
(4) Se quiserem voltar para a visualização inicial, cliquem nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
(b) Aqui estão dois cilindros com a mesma altura.
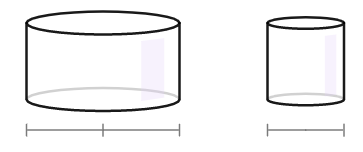
Quantos cilindros pequenos seriam necessários para encher o cilindro grande?
(c) Ajustem a altura para que os objetos tenham o mesmo volume.
(1) Esperem o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar qualquer ponto verde, cliquem sobre ele com qualquer botão do mouse, mantenham o mouse pressionado e façam o movimento. (Se vocês estiverem utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se vocês estiverem usando um computador, vocês também poderão fazer os movimentos dos pontos verdes utilizando os seus teclados: cliquem no ponto a ser movimentado com o botão esquerdo do mouse e, em seguida, façam os movimentos utilizando as teclas “PgUp” ou “PgDn”.
(Para movimentos “mais finos”, mantenham a tecla Shift do teclado apertada enquanto vocês fazem o movimento.)
(4) Se quiserem voltar para a visualização inicial, cliquem nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
(d) Considere um cone e um cilindro com a mesma altura e raio.
Quantos cones seriam necessários para encher o cilindro?
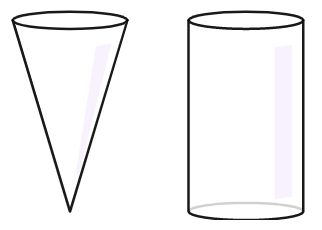
Assim, o volume de um cone de altura h e raio da base r é dado por:
[tex]\qquad \boxed{V=\dfrac{1}{3}\pi r^2\times h}\,.[/tex]
(e) Pesquise a fórmula para o volume de uma esfera.
(f) Ordene os objetos por volume, do menor para o maior.
Observação: Todos têm mesma altura e, para aqueles que possuem diâmetro, a medida do diâmetro é a mesma medida do lado do cubo.
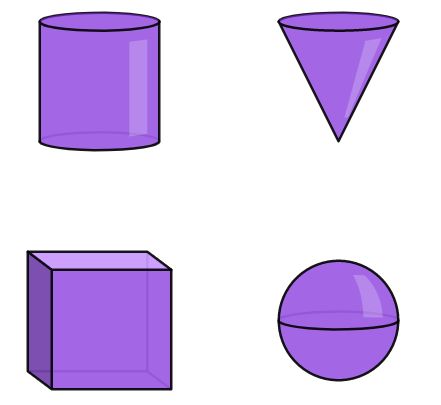
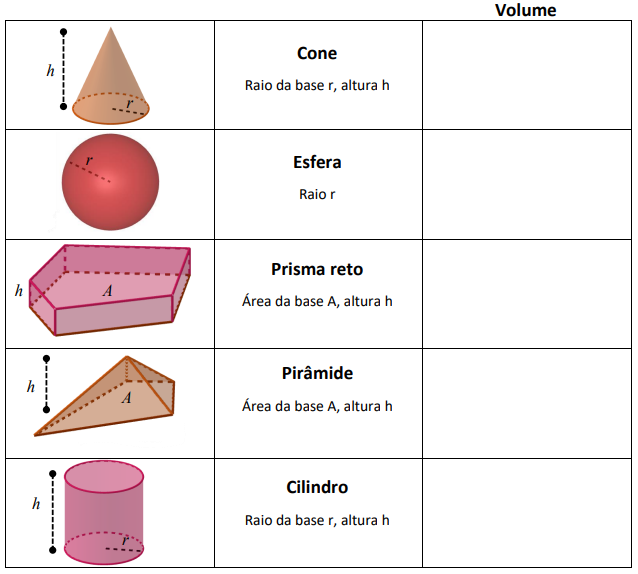
(g) Complete o quadro abaixo (se necessário, peça ajuda ao seu professor de matemática).
Equipe COM – OBMEP
