Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
(XII CONCURSO DE PRIMAVERA DE MATEMÁTICAS, 2008 – adaptado)
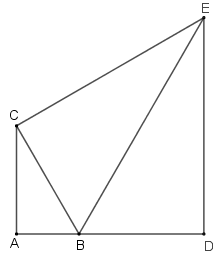
Na figura, [tex]BAC[/tex], [tex]BCE[/tex] e [tex]BDE[/tex] são triângulos retângulos e semelhantes, sendo [tex]B[/tex] um ponto do segmento [tex]AD[/tex].
Se o segmento [tex]CB[/tex] mede [tex]12 \, cm[/tex], qual o comprimento, em centímetros, do segmento [tex]AD[/tex]?
Solução
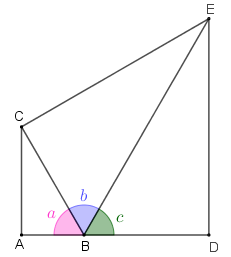
Como os triângulos [tex]BAC[/tex], [tex]BCE[/tex] e [tex]BDE[/tex] são semelhantes, os ângulos de vértices em [tex]B[/tex] e de medidas angulares [tex]a \, [/tex], [tex] \, b \, [/tex] e [tex] \, c \, [/tex] assinalados na figura ao lado são congruentes; assim:
[tex]\qquad a+b+c=180^{\circ}[/tex]
[tex]\qquad a=b=c=\dfrac{180^{\circ}}{3}=60^{\circ}.[/tex]
Para facilitar as próximas análises que faremos, vamos separar os triângulos [tex]BAC[/tex], [tex]BCE[/tex] e [tex]BDE[/tex] e utilizar as medidas em centímetros [tex] \, x \, [/tex], [tex] \, y \, [/tex] e [tex] \, z[/tex] que aparecem nas próximas figuras.
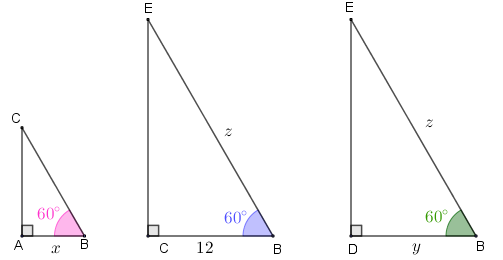
Uma consulta rápida a qualquer tabela trigonométrica nos mostra que [tex]\cos \, 60^{\circ}=\dfrac{1}{2} \, .[/tex]
Observemos essa relação nos triângulos [tex]BAC[/tex], [tex]BCE[/tex] e [tex]BDE[/tex]:
- No triângulo [tex]BAC[/tex]:
[tex]\quad \dfrac{1}{2}=\cos \, 60^{\circ}[/tex]
[tex]\quad \dfrac{1}{2}=\dfrac{x}{12} \, [/tex]
[tex]\quad \textcolor{#DA70D6}{\boxed{x=6 \, cm}} \, .[/tex] - No triângulo [tex]BCE[/tex]:
[tex]\quad \dfrac{1}{2}=\cos \, 60^{\circ}[/tex]
[tex]\quad \dfrac{1}{2}=\dfrac{12}{z} \, [/tex]
[tex]\quad \textcolor{#4169E1}{\boxed{z=24 \, cm}} \, .[/tex] - No triângulo [tex]BDE[/tex]:
[tex]\quad \dfrac{1}{2}=\cos \, 60^{\circ}[/tex]
[tex]\quad \dfrac{1}{2}=\dfrac{y}{z} \, [/tex]
[tex]\quad \dfrac{1}{2}=\dfrac{y}{24} \, [/tex]
[tex]\quad \textcolor{#2E8B57}{\boxed{y=12 \, cm}} \, .[/tex]
Observação: O valor [tex]y=12 \, cm[/tex] poderia ser rapidamente obtido observando-se que os triângulos [tex]ECB \, [/tex] e [tex]EDB \, [/tex] são congruentes, de acordo com o caso de congruência L.A.Ao.( lado – ângulo – ângulo oposto).
Finalmente, perceba que o comprimento do segmento [tex]AD[/tex] é a soma dos comprimentos dos segmentos [tex]AB[/tex] e [tex]BD[/tex], ou seja, [tex]\fcolorbox{black}{#eee0e5}{$x+y=6+12=18 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
