Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Difícil)
Para contar, Renatinha usa apenas os dedos de uma mão e conta de um jeito diferente:
[tex]1 \rightarrow[/tex] dedo polegar; [tex]2 \rightarrow[/tex] dedo indicador; [tex]3 \rightarrow[/tex] dedo médio; [tex]4 \rightarrow[/tex] dedo anelar; [tex]5 \rightarrow[/tex] dedo mínimo; na direção inversa, [tex]6 \rightarrow[/tex] dedo anelar; [tex]7 \rightarrow[/tex] dedo médio; [tex]8 \rightarrow[/tex] dedo indicador; [tex]9 \rightarrow[/tex] dedo polegar.
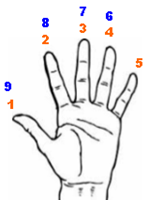
Inverte-se a direção, novamente:
[tex]10 \rightarrow[/tex] dedo indicador; [tex]11 \rightarrow[/tex] dedo médio; [tex]12 \rightarrow[/tex] dedo anelar; [tex]13 \rightarrow[/tex] dedo mínimo; na direção contrária, [tex]14 \rightarrow[/tex] dedo anelar; [tex]15 \rightarrow[/tex] dedo médio; [tex]16 \rightarrow[/tex] dedo indicador; [tex]17 \rightarrow[/tex] dedo polegar.
Se ela prosseguir contando dessa maneira, qual dos dedos da mão de Renatinha será o milésimo?

Solução
Se não quisermos contar até mil utilizando a maneira de contar da Renatinha, vamos ter que encontrar um padrão para essa contagem. Para isso vamos observar que, a cada etapa da contagem a partir da segunda, Renatinha usa o indicador para iniciar e o polegar para terminar uma etapa. Acompanhe a contagem inicial na tabela abaixo:
[tex]\begin{array}{c|c|c|c|c|c|c|c|c|c|c}
po & in & me & an & mi & & an & me & in & \textcolor{#800000}{po} & \\
\hline
1&2&3&4&5&\circlearrowright &6&7&8&\textcolor{#800000}{9}&\circlearrowleft\\
\hline
&10&11&12&13&\circlearrowright &14&15&16&\textcolor{#800000}{17}& \circlearrowleft\\
\hline
&18&19&20&21&\circlearrowright &22&23&24&\textcolor{#800000}{25}& \circlearrowleft\\
\end{array}[/tex]
[tex]\cdots[/tex]
- no início, Renatinha associa ao polegar o número [tex]1[/tex];
- avança quatro dedos, do dedo indicador para o mindinho;
- volta quatro dedos, do dedo anelar para o polegar e associa ao polegar o número [tex]9[/tex];
- inicia um novo ciclo;
- avança quatro dedos, do dedo indicador para o mindinho;
- volta quatro dedos, do dedo anelar para o polegar e associa ao polegar o número [tex]17[/tex];
- … e assim sucessivamente …
Dessa forma, ao final do primeiro ciclo de contagem, ela associa o número nove ao polegar. A partir de então, ao final de cada ciclo da contagem Renatinha associa ao polegar o número anteriormente a ele associado mais [tex]4+4=8[/tex]:
- Primeira etapa: [tex]9=\boxed{1+8} \, [/tex],
- Segunda etapa: [tex]17=9+8=\boxed{1+2×8} \, [/tex],
- Terceira etapa: [tex]25=17+8=\boxed{1+3×8} \, [/tex], e assim por diante.
Pelo até aqui exposto, precisamos determinar, então, em que ciclo o número [tex]1000[/tex] está, para sabermos que dedo a ele será associado. É como se colocássemos os números em caixinhas com oito números cada uma, com exceção da primeira, que terá nove números. Vamos então dividir [tex]1000[/tex] por [tex]8[/tex]:
[tex]\qquad \begin{array}{r}
1000\end{array} \begin{array}{|r}
\, 8 \, \, \\ \hline
\end{array}[/tex]
[tex]\qquad\begin{array}{r}
\, \, \, 0
\end{array}\begin{array}{r}
\, \, \, 125
\end{array}[/tex]
Como [tex]1000[/tex] é divisível por [tex]8[/tex], o polegar será o dedo associado ao número [tex]1001=\boxed{1+125×8} \, [/tex] e o dedo indicador será o milésimo!
[tex]\begin{array}{c|c|c|c|c|c|c|c|c|c|c}
po & in & me & an & mi & & an & me & in & \textcolor{#800000}{po} & \\
\hline
1&2&3&4&5&\circlearrowright &6&7&8&\textcolor{#800000}{9}&\circlearrowleft\\
\hline
&10&11&12&13&\circlearrowright &14&15&16&\textcolor{#800000}{17}& \circlearrowleft\\
\hline
&18&19&20&21&\circlearrowright &22&23&24&\textcolor{#800000}{25}& \circlearrowleft\\
\hline
&& & & &&\cdots&999&\textcolor{red}{1000}&\textcolor{#800000}{1001}&\\
\hline
\end{array}[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
