Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
A partir de quatro quadradinhos com lados unitários, foi montado um quadrado, como o mostrado na figura.
Quantos triângulos não congruentes entre si e com vértices nos nove pontos definidos pelos quatro quadradinhos podem ser formados?

Solução
Como a distância entre dois pontos consecutivos de uma mesma linha ou coluna é [tex]1[/tex], dividiremos a nossa contagem em três casos.
- Caso 1: Triângulos que tenham, pelo menos, um lado com comprimento [tex]1[/tex].

- Caso 2: Triângulos que não tenham lados com comprimentos [tex]1[/tex] e tenham, pelo menos, um lado com comprimento [tex]\sqrt{2}.[/tex]
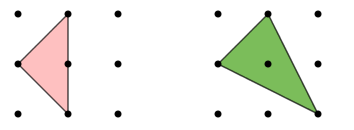
- Caso 3: Triângulos que não tenham lados com comprimentos [tex]1[/tex] e nem lados com comprimentos [tex]\sqrt{2}.[/tex]
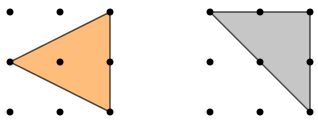
No total temos, então, oito triângulos que podem ser traçados com vértices nos nove pontos da malha [tex]9 \times 9[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
