Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
O jardim da minha casa tem o formato de um "L". Minha mãe dividiu o terreno em três partes, conforme mostra a figura: na região em forma de "V", ela plantou rosas e, no resto do terreno, plantou grama.
Qual a área do terreno onde foram plantadas as rosas?
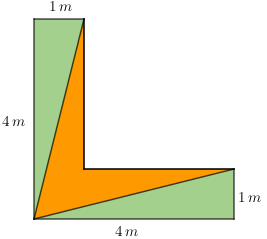
Na figura, considere, hipoteticamente, que os lados do "L" são horizontais ou verticais.
Solução 1
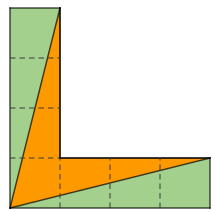
Ao fazermos o desenho do terreno em uma malha quadriculada por quadradinhos unitários, observamos que ao juntarmos os dois triângulos onde a grama foi plantada, obtemos um retângulo de lados [tex]1\,m[/tex] e [tex]4\,m[/tex], cuja área é [tex]4\,m^2.[/tex]
Como a área total do jardim é [tex]7\,m^2[/tex], então a área do terreno onde foram plantadas as rosas é:
[tex]\qquad A_{rosas}=7-4= \fcolorbox{black}{#eee0e5}{$3\,m^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Se você não conseguiu enxergar a junção proposta na Solução 1, podemos calcular diretamente as áreas dos triângulos [tex]T_1[/tex] e [tex]T_2[/tex] que aparecem na próxima figura e subtrai-las da área total do terreno que é [tex]7\,m^2.[/tex]

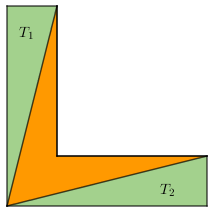
Perceba que os dois terrenos têm a mesma área [tex]A[/tex]:
[tex]\qquad A=\dfrac{4 \times 1}{2}=2\, m^2[/tex].
Assim, a área do terreno onde foram plantadas as rosas é:
[tex]\qquad A_{rosas}=7-2 \times 2 = 7-4= \fcolorbox{black}{#eee0e5}{$3\,m^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 3
Poderíamos, simplesmente, calcular as áreas dos triângulos [tex]T_3[/tex] e [tex]T_4[/tex].
Para isso, talvez observar a figura do jardim sob um ângulo diferente ajude a perceber que [tex]T_3[/tex] e [tex]T_4[/tex] são obtusângulos e têm a mesma área [tex]S[/tex]:
[tex]\qquad S=\dfrac{3 \times 1}{2}=\dfrac{3}{2}\, m^2.\\
\, \, [/tex]
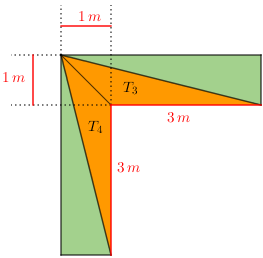

Logo, a área do terreno onde foram plantadas as rosas é:
[tex]\qquad A_{rosas}=2 \times S=2 \times \dfrac{3}{2} = \cancel{2} \times \dfrac{3}{\cancel{2}}= \fcolorbox{black}{#eee0e5}{$3\,m^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
