Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
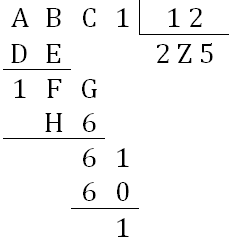
Determinar a soma dos algarismos do dividendo da divisão indicada abaixo.
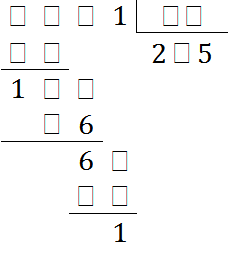
Os números representados pelos quadradinhos não são necessariamente iguais.
Solução
Para facilitar a discussão, vamos dar nome a cada quadradinho e executar os passos da divisão.
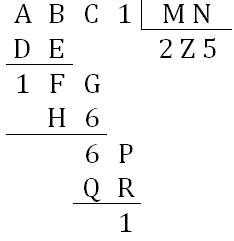

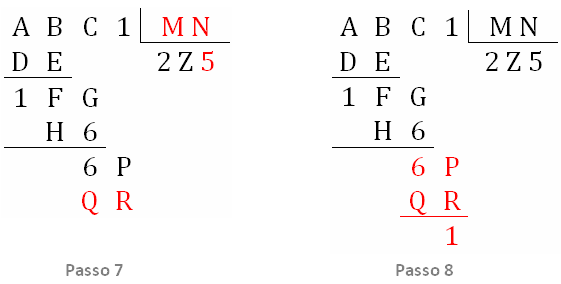
A figura ao lado mostra o nosso progresso! |
[tex]\qquad \textcolor{red}{\begin{array}{r l} 6&1\\ Q&R\\ \hline &1 \end{array}}[/tex]
|
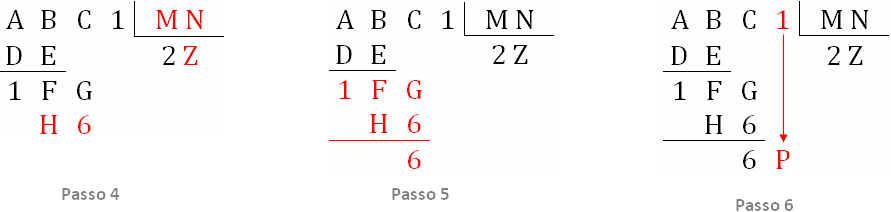
- O Passo 4 indica que [tex]Z \times MN=H6[/tex]; mas, como [tex]MN=12[/tex], [tex]Z \times 12=H6[/tex].
Assim, considerando o algarismo da unidade de [tex]H\textcolor{blue}{6}[/tex], temos duas possibilidades para [tex]Z[/tex]: ou [tex]Z=3[/tex] ou [tex]Z=8[/tex], uma vez que [tex]2\times 3=6[/tex], [tex]2\times 8=16[/tex] e nenhum outro algarismo multiplicado por [tex]2[/tex] resulta em um número cuja unidade seja [tex]6[/tex]. Dessa forma, [tex]H6=Z \times 12=3 \times 12=36[/tex] ou [tex]H6=Z \times 12=8 \times 12=96[/tex] e é o Passo 5 que vai decidir esse impasse. Observe como.
Efetuando essa soma, ficamos com:
[tex]\qquad \begin{array}{c c c }
&H&6\\
&&6\\
\hline
1&F&G
\end{array}[/tex]+ [tex]\qquad \begin{array}{c c c }
&H^1&6\\
&&6\\
\hline
1&F&2
\end{array}[/tex]+
Com isso já temos definido o algarismo [tex]G[/tex], [tex]\boxed{G=2}[/tex], e concluímos que [tex]H+1 \geqslant 10[/tex], já que na coluna das dezenas fica [tex]F[/tex] e “vai um” (com um pouco mais de rigor, [tex]H+1=10+F[/tex]). De qualquer forma, [tex]H \geqslant 9[/tex] e, das duas opções, [tex]H6=36[/tex] ou [tex]H6=96[/tex], resta apenas [tex]H6=96[/tex], e [tex]\boxed{H=9}.[/tex] Consequentemente, [tex]\boxed{Z=8}[/tex] e [tex]\boxed{F=0}.[/tex]
Nosso progresso:
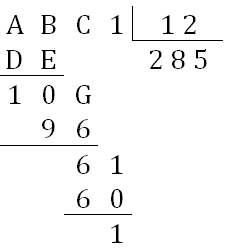
Sabemos que
[tex]\qquad \textcolor{#800000}{ \text{Dividendo= quociente}\times \text{divisor + resto}} [/tex];
assim:
[tex]\qquad \textcolor{#800000}{ \text{Dividendo}=285 \times 12 +1} [/tex]
[tex]\qquad \textcolor{#800000}{ \text{Dividendo}=3421} [/tex]
e, portanto, a soma dos algarismos do dividendo é [tex]\fcolorbox{black}{#eee0e5}{$10$}.[/tex]
Para completar a divisão, basta observar que:
- o Passo 3 mostra que [tex]C=G[/tex] e, assim, [tex]\boxed{G=2}[/tex];
- pelo Passo 1, temos que [tex]2\times MN=DE[/tex]. Mas sendo [tex] MN=12[/tex], [tex]DE=2\times 12=24.[/tex]
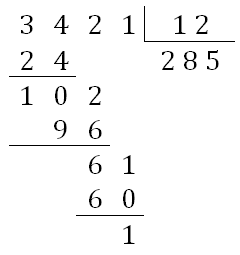
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |