Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
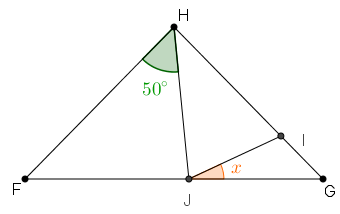
Na figura, [tex]HF=HG[/tex], [tex]HJ=HI[/tex] e [tex]F, \, J, \, G[/tex] são pontos colineares.
Calcule a medida angular [tex]x[/tex].

Lembretes
Alguns resultados sobre ângulos :
[tex] \color{#800000}{(i)}[/tex] A medida de um ângulo externo a um triângulo qualquer é a soma das medidas dos ângulos internos do triângulo que não são adjacentes ele.
[tex] \color{#800000}{(ii)}[/tex] Ângulos da base de um triângulo isósceles têm a mesma medida.
Solução
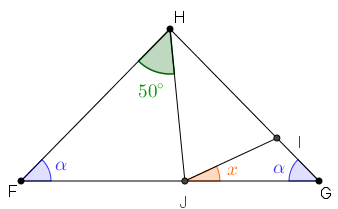
- Observe inicialmente que, como [tex]HF=HG[/tex], então o triângulo [tex]HFG[/tex] é isósceles e, por [tex] \color{#800000}{(ii)}[/tex], os ângulos [tex]\angle{HFG} \, [/tex] e [tex] \, \angle{HGF}[/tex] têm a mesma medida angular, digamos [tex]\boxed{\textcolor{#3333FF}{\alpha}}.[/tex]
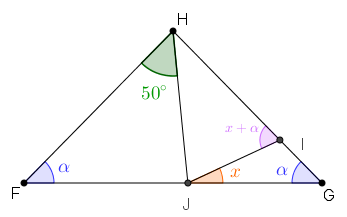
- Note, agora, que [tex]\angle{HIJ} \, [/tex] é um ângulo externo do triângulo [tex]IJG[/tex]; dessa forma, por [tex] \color{#800000}{(i)}[/tex], temos que a medida do ângulo [tex]\angle{HIJ} \, [/tex]é dada por [tex]\boxed{\textcolor{#CC66FF}{x+\alpha}} \, [/tex].
- Mas, por hipótese, [tex]HJ=HI[/tex], logo o triângulo [tex]JHI[/tex] é isósceles e, consequentemente, a medida do ângulo [tex]\angle{HJI} \, [/tex]é também [tex]\boxed{\textcolor{#CC66FF}{x+\alpha}} \, [/tex], por [tex] \color{#800000}{(ii)}[/tex], novamente.
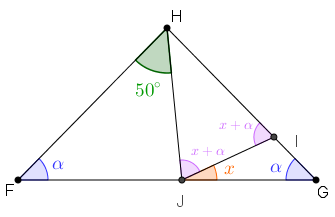
Finalmente, perceba que [tex]\angle{HJG} \, [/tex] é um ângulo externo ao triângulo [tex]HJF[/tex], assim, novamente por [tex] \color{#800000}{(i)}[/tex], temos que [tex]\boxed{(x+\alpha)+x=\alpha + 50^\circ},[/tex] donde segue que:
[tex]\qquad \qquad x+\cancel{\alpha}+x=\cancel{\alpha} + 50^\circ[/tex]
[tex]\qquad \qquad 2x= 50^\circ[/tex]
[tex]\qquad \qquad \fcolorbox{black}{#ffac75}{$x= 25^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
