Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
Um terreno de formato retangular [tex]ABCD[/tex] será dividido em cinco partes, conforme mostra a figura.
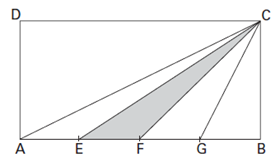
Os pontos [tex]E[/tex], [tex]F[/tex] e [tex]G[/tex] dividem a base [tex]AB[/tex] em quatro partes iguais. As regiões [tex]AEC[/tex], [tex]EFC[/tex], [tex]FGC[/tex] e [tex]GBC[/tex] serão utilizadas para o cultivo de banana, abacaxi (parte destacada), uva e maçã, respectivamente.
Qual é a razão entre a área destinada ao cultivo de abacaxi e a área total do terreno?
Solução
Sejam [tex]x[/tex] e [tex]y[/tex] as medidas dos lados do terreno em questão.
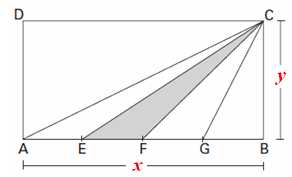
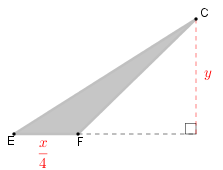
Observe que a área destinada ao plantio de cada fruta, em particular ao plantio de abacaxis, é definida por um triângulo de base [tex]\dfrac{x}{4}[/tex] e altura [tex]y[/tex].
Assim, se denotarmos essa área por [tex]A_a[/tex], então
[tex]\qquad \qquad \boxed{A_a=\dfrac{\frac{x}{4}\cdot y}{2}=\dfrac{x \cdot y}{8}}[/tex].
Como a área total do terreno é dada por [tex]\boxed{A=x \cdot y}[/tex], então:
[tex]\qquad \qquad \dfrac{A_a}{A}=\dfrac{\dfrac{x \cdot y}{8}}{x \cdot y}=\dfrac{\cancel{x \cdot y}}{\cancel{x \cdot y} \cdot 8}=\dfrac{1}{8}[/tex].
Deste modo, a razão entre a área destinada ao cultivo de abacaxi e a área total do terreno é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{A_a}{A}=\dfrac{1}{8}$} \, [/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
