Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Um foguete tripulado chega a um planeta, que fora habitado por seres inteligentes, e lá um livro é encontrado. Ao pé de cada página há um ou mais símbolos que nossos exploradores do espaço supõem serem registros numéricos.
A partir da primeira, as páginas estavam “numeradas” com os símbolos que reproduzimos abaixo, na ordem que eles apareciam e separados por vírgulas.

Supondo que os habitantes do planeta utilizavam um sistema de numeração posicional,
(a) qual seria a base desse sistema?
(b) como estariam “numeradas” as dez próximas páginas desse livro?
(c) escrevam [tex]103[/tex] utilizando o sistema de numeração alienígena.
Solução
(a) A base de um sistema de numeração nada mais é que a quantidade de algarismos utilizados para escrever todos os números. Neste sistema podemos identificar sete símbolos distintos:
![]()
O símbolo com o formato da Lua corresponde ao número [tex]0[/tex], os valores dos demais símbolos são determinados pela quantidade de traços que cada um tem:
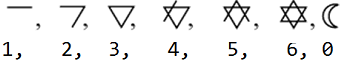
(b) Como se trata de páginas de um livro, estas estariam numeradas em ordem crescente e a partir do símbolo que representa o algarismo [tex]1[/tex] (já que não faz sentido termos uma página zero em um livro).
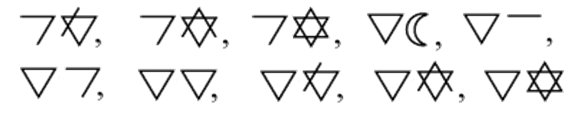
Observe que os números da primeira linha corresponderiam aos nossos algarismos de [tex]1[/tex] a [tex]6[/tex], já que, como visto no item (a), a base tratada é a base [tex]7[/tex]. Fazendo a correlação entre os nossos algarismos e os símbolos do sistema, o último símbolo apresentado corresponderia a [tex](23)_7[/tex], então os dez seguintes seriam:
[tex]\qquad \qquad (24)_7, (25)_7, (26)_7, (30)_7, (31)_7, (32)_7, (33)_7, (34)_7, (35)_7, (36)_7[/tex]
Observação: A notação [tex](ab)_7[/tex] significa que o número está na base [tex]7[/tex].
Tais números na notação do sistema ficariam, respectivamente, como mostra a seguinte imagem:
(c) Deve-se, primeiramente, converter o número [tex]103[/tex] para a base [tex]7[/tex]; para isso realizam-se divisões por [tex]7[/tex] do número e em seguida dos quocientes, até que não seja mais possível realizar as divisões (Ou seja, quando o quociente obtido for menor do que [tex]7[/tex]). Em seguida, junta-se o último quociente e os restos, do final para o início, como a seguir:
|
[tex] \begin{array}{c} 103 \, \, \end{array} \begin{array}{|c} \, \, 7 \, \, \\ \hline \end{array}[/tex] [tex]\begin{array}{c} \boxed{\textcolor{green}{5}} \end{array}\begin{array}{c} \, \, \, \, 14 \end{array}[/tex] |
[tex]\qquad \begin{array}{c} 14 \, \, \end{array} \begin{array}{|c} \, \, 7 \, \, \\ \hline \end{array}[/tex] [tex]\qquad \begin{array}{c} \boxed{\textcolor{blue}{0}} \end{array}\begin{array}{c} \, \, \, \, \boxed{\textcolor{red}{2}} \end{array}[/tex] |
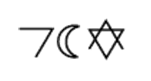
Então [tex](103)_{10} = (\textcolor{red}{2}\textcolor{blue}{0}\textcolor{green}{5})_7[/tex].
Agora, é só substituir os algarismos convertidos pelos símbolos dos extraterrestres:
Compilação de soluções elaboradas pelos seguintes alunos do PIC 2017, com algumas contribuições dos Moderadores do Blog: EVERTON ALBUQUERQUE DE OLIVEIRA ; MARIA EDUARDA RAMOS PEREIRA ; THIAGO SOUSA BEZERRA.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
