Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F.) (Nível: Fácil)
Uma calçada com um metro de largura foi construída em volta de uma piscina retangular, de modo que suas bordas ficassem paralelas às bordas da piscina.
Sabendo que a área total da calçada é [tex]50 \, m^2[/tex], qual é o perímetro da piscina?
Solução
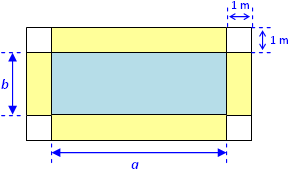
Observe que a área da calçada em torno da piscina é igual a soma "das áreas dos quatro cantos quadrados com a área dos quatro retângulos amarelos" indicados na figura abaixo.
- Como a área total da calçada é [tex]50 \, m^2[/tex] e a área de cada canto é [tex]1 \, m^2[/tex], então a área dos quatro retângulos amarelos é [tex]50-4\times 1=50-4=46 \, m^2[/tex].
Se [tex] \, a \, [/tex] e [tex] \, b \, [/tex] são as dimensões da piscina, conforme mostra a figura abaixo, então temos que [tex]46=2\left(a\cdot 1\right)+2\left(b\cdot 1\right)[/tex], já que a largura das calçadas é [tex]1 \, m[/tex].
Dessa forma, [tex]46=2\cdot a+2 \cdot b[/tex] e, portanto, o perímetro da piscina é [tex]46 \, m[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
