Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F.) (Nível: Médio)
As flores de Geometrix têm formatos interessantes.
Algumas delas possuem a forma mostrada na figura, na qual há seis quadrados e doze triângulos equiláteros.
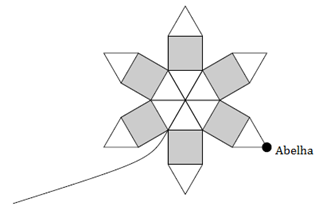
Uma abelha pousou no ponto destacado e andou sobre a borda da flor, no sentido horário, até voltar ao ponto de onde partiu.
Sabendo que a região cinza tem [tex]54 \, \text{cm}^2[/tex] de área, qual é a distância percorrida pela abelha?
Solução
Observe que, como os triângulos internos da figura são equiláteros, todos têm lados com mesmo comprimento,
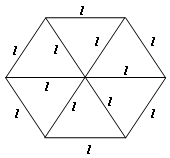
dessa forma, os lados dos quadrados e dos triângulos têm todos o mesmo comprimento.
Assim, a área da região cinza corresponde à soma das áreas de seis quadrados congruentes e, portanto, cada quadrado possui:
- [tex]9 \, \text{cm}^2[/tex] de área;
- lados com [tex]\sqrt{9}=3 \, \text{cm}[/tex] de comprimento.
Como os lados dos quadrados e dos triângulos são todos iguais, a abelha percorrerá quatro segmentos com comprimento [tex]3 \, \text{cm}[/tex] para ir de um vértice externo de um triângulo a outro consecutivo, ou seja, percorrerá [tex]4 \times3 =12 \, \text{cm}[/tex] entre dois vértices externos consecutivos.
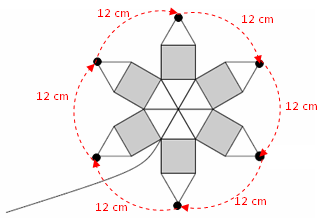
Portanto, uma volta completa da abelha em torno da flor corresponde a [tex]6 \times 12 \, \text{cm}[/tex], ou seja, a abelha percorrerá [tex]\boxed{72 \, \text{cm}}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
