Clique no botão abaixo para visualizar o texto.
Setor circular e segmento circular
 |
Vamos discutir sobre duas regiões de um círculo que, embora sejam bastante utilizadas na solução de problemas envolvendo áreas, é comum certa confusão entre elas. Ambas as regiões dependem de uma circunferência e de um ângulo central (ou um arco de circunferência), elas têm uma relação entre si, mas são objetos matemáticos distintos. |
Setor Circular
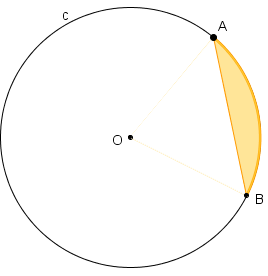
Chamamos de setor circular a região do círculo [tex]c[/tex] limitada pelo arco da circunferência definido por [tex]A[/tex] e [tex]B[/tex] e pelos raios [tex]OA[/tex] e [tex]OB[/tex].
Se [tex]A[/tex] e [tex]B[/tex] não forem extremidades de um diâmetro, o setor circular definido pode receber nomes particulares: o setor é chamado de setor circular menor, se o arco que o define for o chamado “arco menor”; caso contrário, o setor é dito setor circular maior.
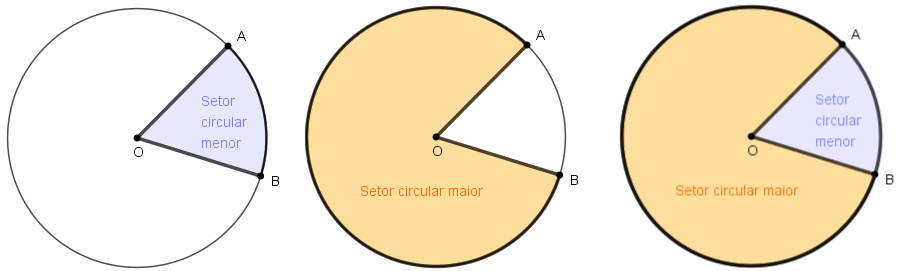
De modo geral, o arco utilizado na definição de um setor circular é o dito “arco menor”; assim, quase todas as nossas figuras mostram setores circulares definidos por arcos menores, mas as conclusões aqui estabelecidas são válidas para setores circulares definidos por arcos quaisquer. Observe que, em um mesmo círculo, a soma das áreas do setor circular maior e do setor circular menor definidos pelos pontos [tex]A[/tex] e [tex]B[/tex] é exatamente a área do próprio círculo.
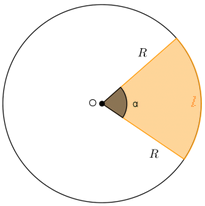
| Perceba que os raios [tex]OA[/tex] e [tex]OB[/tex] e o centro [tex]O[/tex] definem um ângulo central e um arco. Assim, podemos associar a cada setor circular três medidas: o comprimento [tex]R[/tex] do raio do círculo, a medida [tex]\alpha[/tex] do ângulo central e o comprimento [tex]l [/tex] do arco. Sendo uma região do plano, o setor circular tem uma área que pode ser calculada se conhecemos a medida [tex]R[/tex] e a medida [tex]\alpha[/tex] (em radianos ou em graus). Se conhecermos o comprimento do arco definido pelos pontos [tex]A[/tex] e [tex]B[/tex], além do comprimento [tex]R[/tex] do raio, também é possível obtermos a área do setor circular. |
 |
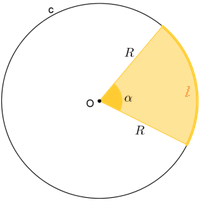 |
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] radianos
[tex]\qquad \qquad\boxed{A_{setor}=\dfrac{\alpha R^{ \, 2}}{2}}[/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus
[tex]\qquad \qquad \boxed{A_{setor}=\dfrac{\pi R^{ \, 2} \alpha}{360}}[/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e comprimento de arco [tex]l[/tex]
[tex]\qquad \qquad\boxed{A_{setor}=\dfrac{l\cdot R}{2}}[/tex]
Para saber de onde vieram essas três fórmulas, clique no botão abaixo.
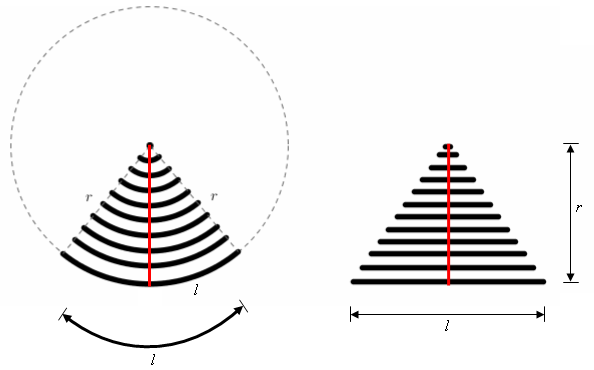
O setor circular é uma parte do círculo que o define e sua área depende diretamente da medida do ângulo central ou do comprimento de arco a ele associado. Podemos, então, calcular a área de um setor circular aplicando uma regra de três simples já que esta área será uma porcentagem da área do círculo que o define: [tex]\pi R^2 [/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] radianos
A regra de três simples
| [tex]2\pi \, rad[/tex] | ————————————– | [tex]\pi R^2[/tex] |
| [tex]\alpha \, rad [/tex] | ————————————– | [tex]A_{setor}[/tex] |
garante que [tex]\boxed{A_{setor}=\dfrac{\alpha R^{ \, 2}}{2}}[/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus
A regra de três simples
| [tex]360^{\circ}[/tex] | ————————————– | [tex]\pi R^2[/tex] |
| [tex]\alpha^{\circ} [/tex] | ————————————– | [tex]A_{setor}[/tex] |
garante agora que [tex]\boxed{A_{setor}=\dfrac{\pi R^{ \, 2} \alpha}{360}}[/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e comprimento de arco [tex]l[/tex]
Mais uma regra de três simples:
| [tex]2\pi R[/tex] | ————————————– | [tex]\pi R^2[/tex] |
| [tex]l [/tex] | ————————————– | [tex]A_{setor}[/tex] |
Temos, agora, que [tex]\boxed{A_{setor}=\dfrac{l\cdot R}{2}}[/tex]
Achou a última fórmula parecida com a da área de um triângulo?
Então, clique no botão abaixo.
Segmento Circular
Chamamos segmento circular a região do círculo [tex]c[/tex] limitada pela corda e pelo arco da circunferência definidos por [tex]A[/tex] e [tex]B[/tex].
Se [tex]A[/tex] e [tex]B[/tex] não forem extremidades de um diâmetro, o segmento circular definido também pode receber nomes particulares: se o arco que define o segmento circular for o chamado “arco menor”, então temos o segmento circular menor, caso contrário, temos um segmento circular maior.
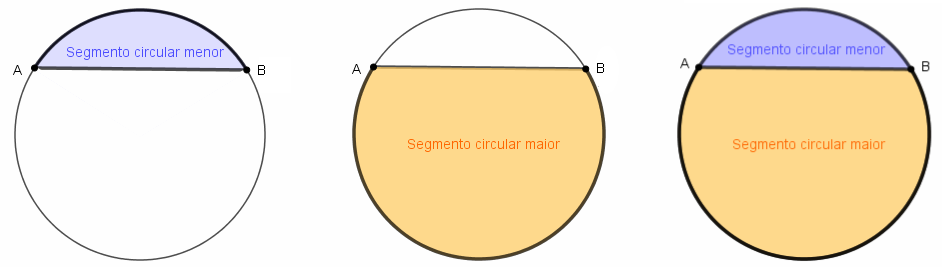
De modo geral, o arco utilizado na definição de um segmento circular é também o “arco menor”; assim, quase todas as nossas figuras mostram setores circulares definidos por arcos menores. Observe que, em um mesmo círculo, a soma das áreas do segmento circular maior e do segmento circular menor definidos pelos pontos [tex]A[/tex] e [tex]B[/tex] é igual à área do próprio círculo.
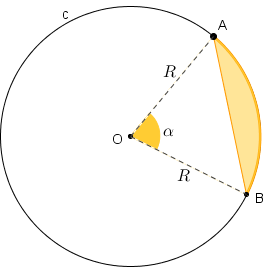
| Perceba que os pontos [tex]O[/tex], [tex]A[/tex] e [tex]B[/tex] definem os raios [tex]OA[/tex] e [tex]OB[/tex] e um ângulo central. Assim, podemos associar a cada segmento circular duas medidas: o comprimento [tex]R[/tex] do raio do círculo e a medida [tex]\alpha[/tex] do ângulo central. Sendo também uma região do plano, o segmento circular tem uma área que pode ser calculada se conhecemos a medida [tex]R[/tex] e a medida [tex]\alpha[/tex] em radianos. |
|
|
✐ Área de um segmento circular de raio [tex]R[/tex] e [tex]\alpha[/tex] radianos
[tex]\qquad \qquad \boxed{A_{segm}=\dfrac{R^{ \, 2}}{2}\left(\alpha-sen \, \alpha\right)}[/tex]
Para saber de onde veio essa fórmula, clique no botão abaixo.
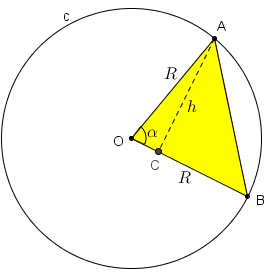
Observe que a área do segmento circular é dada pela diferença entre a área do setor circular e a área do triângulo [tex] OBC[/tex].
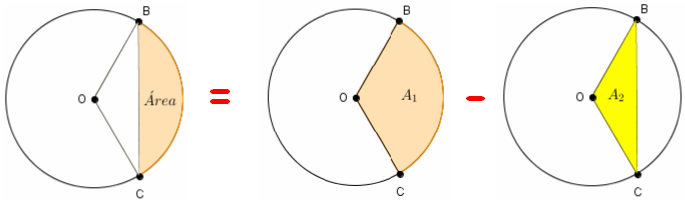
Assim, [tex]\acute{A}rea=A_1-A_2[/tex], onde
- [tex]\acute{A}rea[/tex]: área do segmento circular;
- [tex] A_1[/tex]: área do setor circular;
- [tex] A_2[/tex]: área do triângulo [tex] OBC[/tex].
Já sabemos que [tex]A_1=\dfrac{\alpha R^2}{2}[/tex]; assim, basta encontrarmos [tex]A_2[/tex]. Então, vamos lá!
Note que [tex]A_2[/tex] é a área de um triângulo, então [tex]A_2=\dfrac{base \times altura}{2}[/tex].
Observe a próxima figura e siga a dedução.
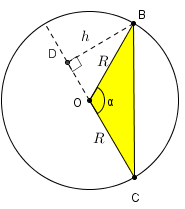
|
Como [tex]A_2=\dfrac{R \times h}{2} [/tex], precisamos obter uma expressão para [tex]h[/tex] em termos dos dados conhecidos: [tex]R[/tex] e [tex]\alpha[/tex]. Como o triângulo [tex]ODB[/tex] é retângulo, então [tex]sen(\pi-\alpha)=\dfrac{h}{R} \, [/tex] e, assim, [tex]\quad \boxed{h= R \, sen(\pi-\alpha)}[/tex]. Mas [tex]\alpha[/tex] e [tex]\pi -\alpha[/tex] são medidas de ângulos suplementares, logo [tex]\quad sen \, \alpha=sen \, (\pi -\alpha)[/tex]. |
|
Dessa forma, [tex]h= R \, sen \, \alpha[/tex] e, portanto:
[tex]\quad A_2 =\dfrac{R \times h}{2}[/tex]
[tex]\quad A_2 =\dfrac{R \times R sen \, \alpha}{2}[/tex]
[tex]\quad A_2 =\dfrac{R^2 sen \, \alpha}{2}[/tex] |
Observe que se o ângulo [tex]\alpha[/tex] fosse agudo, a altura [tex]h= R \, sen \, \alpha[/tex] do triângulo [tex]ABO[/tex] seria mais facilmente obtida; observe:
[tex]\quad sen \, \alpha =\dfrac{\text{cateto oposto}}{\text{hipotenusa}}[/tex]
[tex]\quad sen \, \alpha= \dfrac{h}{R} [/tex]
[tex]\quad h= R \, sen \, \alpha[/tex] |
Pronto, finalmente podemos calcular a área do segmento circular:
[tex]\quad \acute{A}rea \, \, = A_1-A_2 [/tex]
[tex]\qquad \qquad =\dfrac{\alpha R^{ \, 2}}{2}-\dfrac{R^{ \, 2} sen \, \alpha}{2}[/tex]
[tex]\qquad \qquad =\dfrac{R^{ \, 2}}{2}\left(\alpha- sen \, \alpha\right).[/tex]
Portanto, [tex]\boxed{{A_{segm}=\dfrac{R^{ \, 2}}{2}\left(\alpha-sen \, \alpha\right)}}[/tex]
 |
Esperamos que você tire proveito da explanação feita aqui. |
Sonia Regina Di Giacomo
Equipe COM – OBMEP