Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.) (Nível: Fácil)
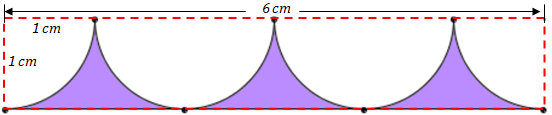
Na figura, todos os arcos foram definidos por circunferências de raio [tex]1 \, cm[/tex] e os pontos destacados definem quadrantes ou semicircunferências, de modo que os arcos limitados por dois pontos consecutivos são de noventa graus.

Calcule a área da região destacada.
Solução
Considere o retângulo definido pelos pontos destacados nos arcos; a área desse retângulo é [tex]6 \, cm^2[/tex].
Perceba que, se [tex]S[/tex] for área do círculo de raio [tex]1 \, cm[/tex], então [tex]S=\pi\cdot (1)^2=\pi \, cm^2[/tex] e a área [tex]A[/tex] da região destacada é dada por
[tex]\qquad A=6-\dfrac{S}{4}-\dfrac{S}{2}-\dfrac{S}{2}-\dfrac{S}{4}[/tex],
conforme ilustra a figura abaixo.

Dessa forma:
[tex]\qquad \begin{align*}A&=6-\left(\dfrac{S}{4}+\dfrac{S}{2}+\dfrac{S}{2}+\dfrac{S}{4}\right)\\
&=6-\dfrac{6S}{4}\\
&=6-\dfrac{3S}{2}\\
&=6-\dfrac{3\pi}{2}. \end{align*}[/tex]
Portanto a área da figura destacada é [tex] \fcolorbox{black}{#eee0e5}{$\dfrac{12-3\pi}{2} \, cm^2$}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
