Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
Como podemos construir um pentágono regular com lados medindo [tex]4 \, [/tex]cm, usando apenas uma régua e um transferidor, além de, obviamente, lápis, papel e borracha… ?
Justifique os passos da construção.

Solução
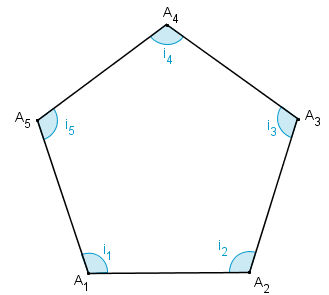
Na construção do pentágono só poderemos utilizar como instrumentos de construção uma régua e um transferidor; assim, com a régua traçaremos os lados do pentágono e com o transferidor mediremos os seus ângulos internos. Os lados sabemos que medem [tex]4 \, [/tex]cm cada; mas quanto mede cada ângulo interno de um pentágono regular?
A resposta é simples para quem conhece a soma das medidas dos ângulos internos de um pentágono, que denotaremos por [tex]S_5[/tex].
➤ Como [tex]S_5=540^{\circ}[/tex] e o pentágono é regular, então os seus cinco ângulos internos têm a mesma medida:
[tex]\qquad \qquad a_i=\dfrac{540^{\circ}}{5}=108^{\circ}[/tex].
Pronto! Você já está apto(a) a fazer a construção do pentágono.
Precisa de uma ajudinha?
Clique no botão abaixo, aguarde o aplicativo carregar
e veja um gif animado da construção.

Precisa de mais ajuda?
Então utilize um applet.
É só clicar no próximo botão e seguir as instruções.
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Clique ordenadamente nos quadradinhos até completar a construção.
3) Para reiniciar a construção, clique nas setinhas que aparecem no canto superior direito do applet.
Para carregar o applet, clique AQUI
OBMEP_ srdg, criado com o GeoGebra
Não sabe por que [tex]S_5=540^{\circ}[/tex]?
Clique no próximo botão…
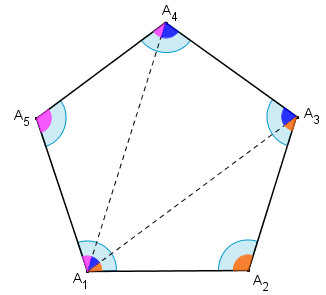
A partir do vértice [tex]A_1[/tex], tracemos as diagonais [tex]\overline{A_1A_3} \, [/tex] e [tex]\overline{A_1A_4} \, [/tex]. Com isso, o polígono fica dividido em três triângulos.
Perceba que a soma [tex]S_5[/tex] dos ângulos internos do polígono,
[tex]\qquad S_5=i_1+ i_2+ i_3+ i_4+ i_5[/tex],
é igual à soma dos ângulos internos dos três triângulos.
Como a soma dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], concluímos que
[tex]\qquad S_5=3 \times 180^{\circ}[/tex],
ou seja,
[tex]\qquad \boxed{S_5=540^{\circ}}[/tex].
Solução elaborada pelos Moderadores do Blog.
