✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 3º ano do E. M.)
Considere todos os pares de números reais [tex]x[/tex] e [tex]y[/tex] para os quais [tex]x^{2}+y^{2}=1[/tex]. Neste conjunto, encontre o maior valor assumido pela expressão [tex]E = x + 2y.[/tex]
Extraído de PAPMEM-IMPA – 2014.

Lembretes
(I) O ângulo formado entre a reta tangente e o raio da circunferência é de [tex]90 ^\circ[/tex].
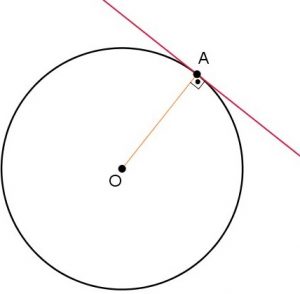
(II) O produto dos coeficientes angulares de retas perpendiculares vale [tex]-1[/tex].
Solução
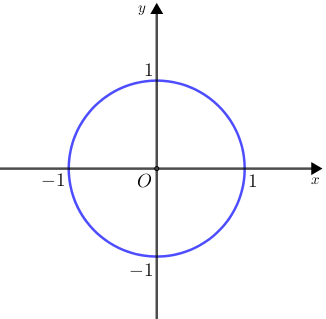
Considerando o plano cartesiano [tex]xOy[/tex], a expressão [tex]\textcolor{blue}{x^{2}+y^{2}=1}[/tex], geometricamente, representa uma circunferência de centro [tex]O=(0,0)[/tex] e raio [tex]1[/tex].
Note que, se [tex]E[/tex] é um número real, a igualdade [tex]E=x+2y[/tex] é equivalente a [tex]y=\dfrac{-x}{2}+\dfrac{E}{2}[/tex].
No plano cartesiano [tex]xOy[/tex], essa última equação representa um feixe de retas paralelas com coeficiente angular [tex]-\dfrac{1}{2}[/tex] e coeficiente linear [tex]\dfrac{E}{2}[/tex].
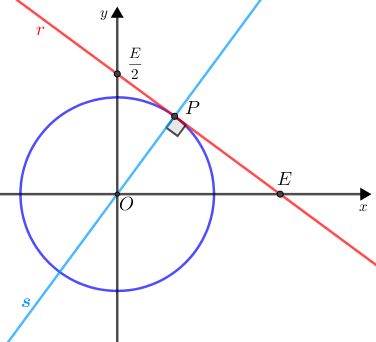
A figura abaixo mostra uma reta [tex]\textcolor{red}{r}[/tex] desse feixe, para um número real positivo [tex]E[/tex] particular. Note que essa reta é decrescente e intercepta o eixo vertical em [tex]\dfrac{E}{2}[/tex] e o eixo horizontal em [tex]E[/tex].
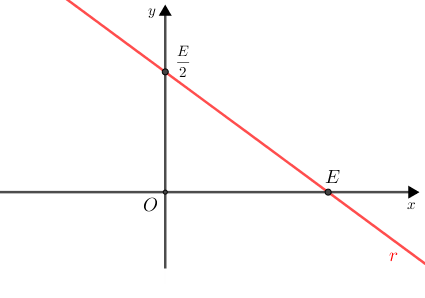
Perceba que, quando [tex]E[/tex] aumenta, a respectiva reta [tex]\textcolor{red}{r}[/tex] afasta-se da origem e, num dado momento, deixará de intersectar a circunferência, o que significa que não estaremos mais dentro das condições do problema.
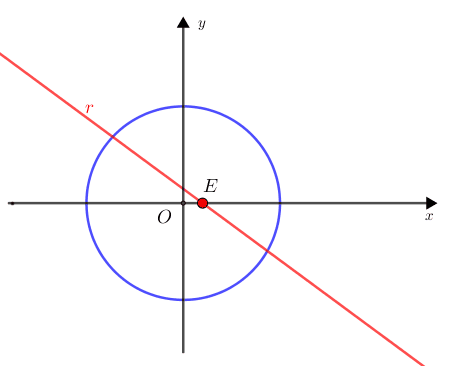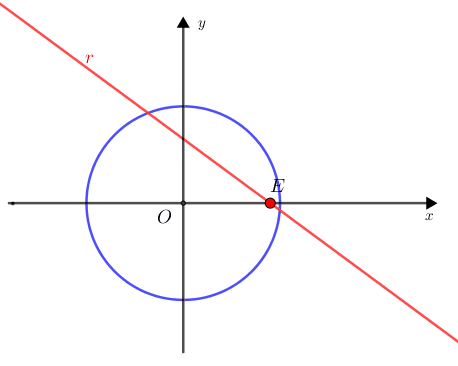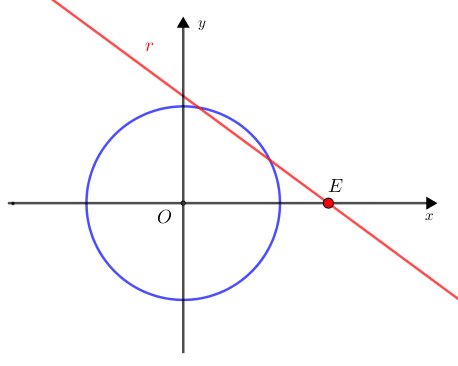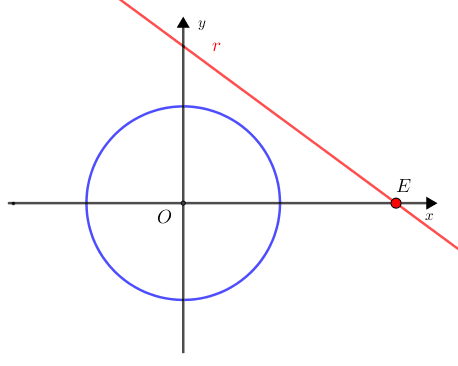
Assim, para que sejam cumpridas as hipóteses do problema, o valor máximo de [tex]E[/tex] ocorrerá quando a reta [tex]\textcolor{red}{r}[/tex] for tangente à circunferência definida por [tex]x^{2}+y^{2}=1[/tex], em um ponto do primeiro quadrante.
Vamos denotar por [tex]P[/tex] esse ponto de tangência.
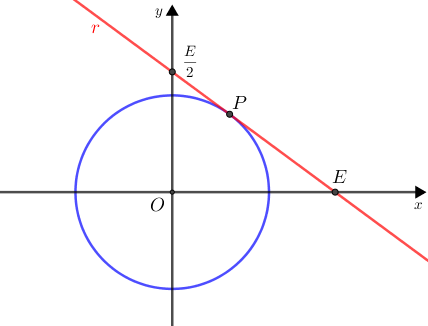
Seja [tex]\textcolor{#0099FF}{s}[/tex] a reta que passa por [tex]O[/tex] e [tex]P[/tex]. Vamos determinar a equação de [tex]\textcolor{#0099FF}{s}[/tex], para podermos determinar as coordenadas do ponto [tex]P[/tex].
- Pelo lembrete (I), a reta [tex]\textcolor{#0099FF}{s}[/tex] é perpendicular à reta [tex]\textcolor{red}{r}[/tex]. Portanto, pelo lembrete (II), o coeficiente angular de [tex]\textcolor{#0099FF}{s}[/tex] é [tex]\boxed{\, -\dfrac{1}{-1/2}=2}\,.[/tex]
- Por outro lado, por passar pelo ponto [tex](0,0)[/tex], o coeficiente linear da reta [tex]\textcolor{#0099FF}{s}[/tex] é igual a [tex]0[/tex].
Sendo assim, a equação de [tex]\textcolor{#0099FF}{s}[/tex] é [tex]y=2x[/tex].
Finalmente, para encontrar o ponto [tex]P[/tex] basta resolver o sistema:
[tex]\qquad \begin{cases} x^{2} + y^{2} = 1 \\ y = 2x \end{cases}~[/tex].
Vamos lá!
Substituindo o valor de [tex]y[/tex] dado pela segunda equação na primeira, segue que:
[tex]\qquad x^{2}+4x^{2}=1 \\
\qquad x^2=\dfrac{1}{5}\\
\qquad x= \pm\dfrac{1}{\sqrt{5}}.[/tex]
Como [tex]P[/tex] é um ponto do primeiro quadrante, [tex]x=\dfrac{1}{\sqrt{5}}\,[/tex] e, portanto, [tex]P=\left(\dfrac{1}{\sqrt{5}}, \dfrac{2}{\sqrt{5}}\right)\,.[/tex]
Assim, finalmente concluímos que:
[tex]\qquad E=\dfrac{1}{\sqrt{5}}+2\cdot\dfrac{2}{\sqrt{5}}=\dfrac{5}{\sqrt{5}}\\
\qquad \,\fcolorbox{black}{#eee0e5}{$E=\sqrt{5}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
