✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir da 1ª série do E. M.)
(PUCCAMP) Em uma turma de uma escola, há [tex]90[/tex] alunos. Eles escolheram de [tex]1[/tex] a [tex]3[/tex] disciplinas optativas dentre as seguintes: Tópicos de Biologia, Tópicos de Geografia, Tópicos de História e Tópicos de Química.
Sabe-se que:
• [tex]48[/tex] alunos escolheram Tópicos de Biologia;
• [tex]12[/tex] escolheram Tópicos de Geografia;
• [tex]55[/tex] escolheram Tópicos de História;
• [tex]14[/tex] escolheram Tópicos de Química;
• Todos os alunos que escolheram Tópicos de Geografia escolheram, também, Tópicos de História;
• Todos os alunos que escolheram Tópicos de Química escolheram, também, Tópicos de Biologia;
• Nenhum dos alunos que escolheu Tópicos de Biologia escolheu, também, Tópicos de Geografia;
• [tex]6[/tex] alunos escolheram [tex]3[/tex] disciplinas optativas.
Nessas condições, calcule o número de alunos que escolheu apenas Tópicos de Biologia e Tópicos de História.
Ajuda
Diagramas de Venn são representações esquemáticas que permitem visualizarmos conjuntos como se fossem regiões do plano.
Podemos utilizar esse tipo de representação para organizar os dados de determinados problemas e visualizar melhor um caminho para resolvê-los. A partir de um conjunto universo, os vários conjuntos envolvidos no problema são limitados por figuras fechadas, como círculos, quadrados, retângulos e losangos. O interior de cada figura representa os elementos do respectivo conjunto.
 |
Para aprender mais sobre o tema, dê uma passadinha nesta Sala do nosso Blog. |
Solução
Pelo enunciado, vemos que este é um típico problema para ser resolvido utilizando Diagramas de Venn para organizar os dados. O diagrama que vamos construir será relativo ao número de alunos que escolheram as disciplinas em questão; assim, a princípio, temos que construir quatro diagramas de conjuntos, já que são quatro as disciplinas optativas. Vamos indicar pelas iniciais B, G, H e Q os conjuntos associados aos alunos que escolheram, respectivamente, Tópicos de Biologia, Tópicos de Geografia, Tópicos de História e Tópicos de Química.
Vamos, inicialmente, traduzir em linguagem de conjuntos alguns dados do problema:
- Todos os alunos que escolheram Tópicos de Geografia escolheram, também, Tópicos de História: [tex]G \subset H[/tex];
- Todos os alunos que escolheram Tópicos de Química escolheram, também, Tópicos de Biologia: [tex]Q \subset B[/tex]
- Nenhum dos alunos que escolheu Tópicos de Biologia escolheu, também, Tópicos de Geografia: [tex]B \cap G= \emptyset[/tex];
- [tex]6[/tex] alunos escolheram [tex]3[/tex] disciplinas optativas: existe uma interseção de três conjuntos.
Ficamos, então, com o diagrama de quatro conjuntos abaixo.
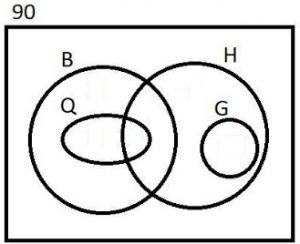
Agora, utilizando os dados numéricos
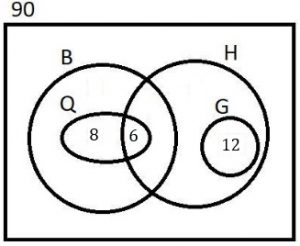
- [tex]6[/tex] alunos escolheram [tex]3[/tex] disciplinas optativas;
- [tex]12[/tex] escolheram Tópicos de Geografia;
- [tex]14[/tex] escolheram Tópicos de Química (escolheram apenas Tópicos de Química e Tópicos de Biologia [tex]14-6=8[/tex] alunos);
podemos preencher parcialmente esse diagrama, conforme mostra a figura abaixo.
Se representarmos por [tex]x[/tex] os alunos que optaram apenas pelas optativas Tópicos de Biologia e Tópicos de História, poderemos utilizar os dados numéricos restantes do enunciado:
- [tex]48[/tex] alunos escolheram Tópicos de Biologia;
- [tex]55[/tex] escolheram Tópicos de História;
e finalizar o preenchimento do diagrama
- [tex]48-8-6-x=34-x[/tex] escolheram apenas Tópicos de Biologia;
- [tex]55-12-6-x=37-x[/tex] escolheram apenas Tópicos de História.
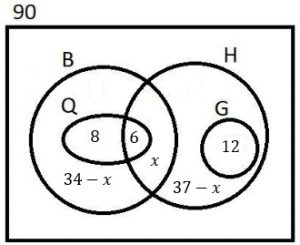
Como na turma existem [tex]90[/tex] alunos, então [tex]8+6+12+(34-x)+x+(37-x)=90[/tex], donde segue que:
[tex]\qquad 8+6+12+34-x+x+37-x=90\\
\qquad 97-x=90\\
\qquad x=7.[/tex]
Portanto, [tex]7[/tex] alunos optaram apenas por Tópicos de Biologia e Tópicos de História.
Solução elaborada pelos Moderadores do Blog.
