✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
(Harvard-MIT) No quadrilátero [tex]ABCD[/tex] que aparece na figura abaixo, [tex]BC=AD[/tex] e as medidas dos ângulos [tex]D\hat A C[/tex], [tex]D\hat B C[/tex] e [tex]B\hat C D[/tex] são, respectivamente, [tex]\color{#993300}{98 ^\circ}[/tex], [tex]\color{red}{82 ^\circ}[/tex] e [tex]\color{#0000FF}{70 ^\circ}[/tex].
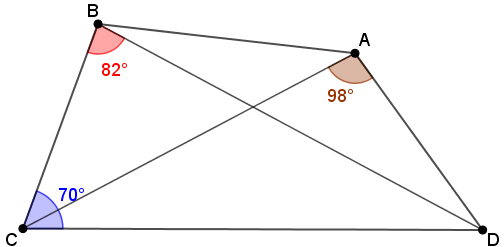
Encontre a medida do ângulo [tex]A\hat C D[/tex].

Lembretes e notações
(1) A soma das medidas dos ângulos internos de qualquer triângulo vale [tex]180^\circ[/tex]. (Se precisar, visite esta página.)
(2) Ângulos Suplementares são ângulos cuja soma resulta em um ângulo raso, cuja medida é [tex]180^\circ[/tex].
(3) Caso de congruência de triângulos L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. (Para aprender mais, visite esta página.)
(4) Em todo triângulo isósceles os ângulos da base possuem a mesma medida.
(5) Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e sua medida por [tex]XY[/tex].
(6) Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]X\hat{V}Y[/tex] e a sua medida por [tex]m(X\hat{V}Y)\,.[/tex]
Solução
Chamemos de [tex]\color{#FF00FF}{\alpha}[/tex] a medida em graus do ângulo [tex]A\hat C D[/tex].
Note que, pelo Lembrete 1, podemos encontrar a medida do ângulo [tex]C\hat DB[/tex]:
[tex]\qquad m(C\hat D B)=180^\circ -(82^\circ+70^\circ)=28^\circ.[/tex]
Agora, vamos prolongar o segmento [tex]\overline{CA}[/tex] até um ponto [tex]E[/tex], de modo que [tex]AE=BD[/tex].
Pelo Lembrete 2, o ângulo [tex]E\hat A D[/tex] é o suplemento de [tex]D\hat A C[/tex]. Assim, [tex]m(E\hat A D)=82^\circ[/tex].
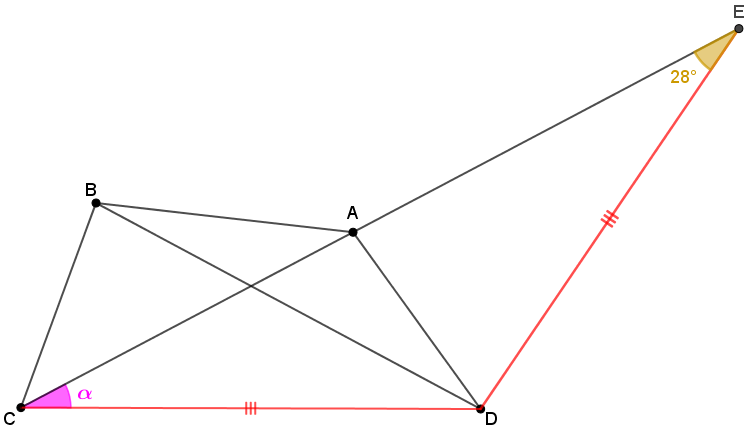
Na imagem a seguir, colocamos os últimos dados encontrados e representamos por verde e azul, respectivamente, os pares de segmentos congruentes.
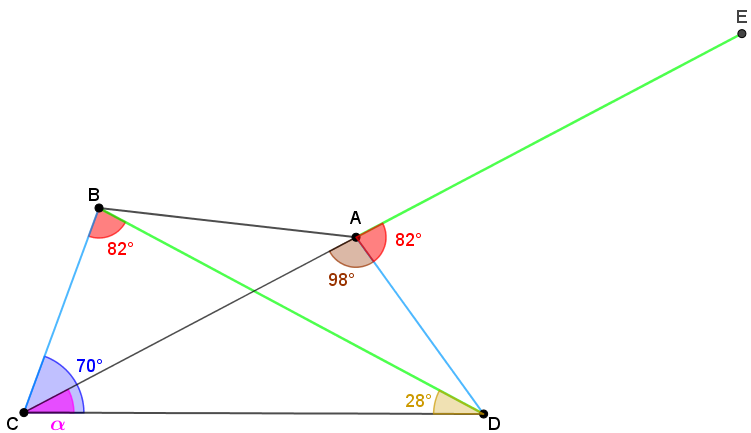
Mas, ao construir o triângulo [tex]EAD[/tex] notamos que, pelo Lembrete 3, ele é congruente ao triângulo [tex]DBC[/tex].
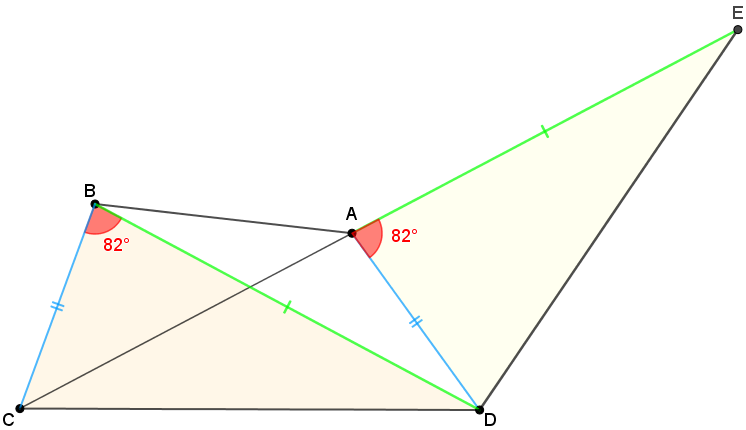
Portanto, [tex]m(D\hat E A)=28^\circ[/tex], [tex]m(A\hat D E)=70^\circ[/tex] e [tex]DE=CD.[/tex]
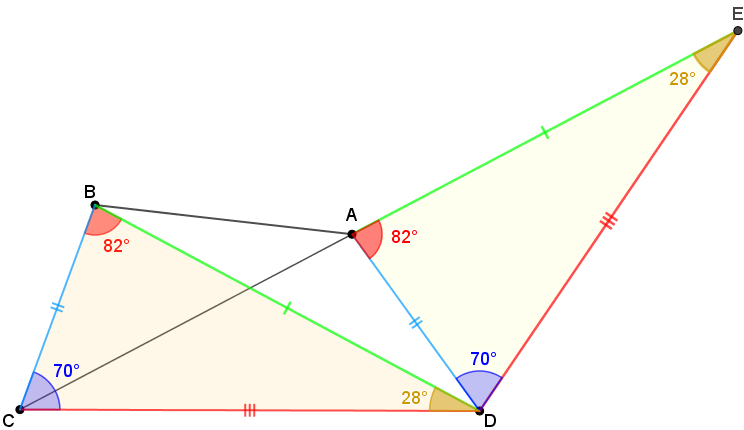
Por fim, observe que o triângulo [tex]ECD[/tex] é isósceles; logo, pelo Lembrete 4, [tex]\color{#FF00FF}{\alpha=28^\circ}[/tex].
Solução elaborada pelos Moderadores do Blog.
