✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2º ano do E. M.)
(UERJ 2016 – Adaptado) Um painel de iluminação possui nove seções distintas, e cada uma delas acende uma luz de cor vermelha ou azul. A cada segundo, são acesas, ao acaso, duas seções de uma mesma cor e uma terceira de outra cor, enquanto as seis demais permanecem apagadas.
Observe quatro diferentes possibilidades de iluminação do painel:
Qual o tempo mínimo necessário, em minutos, para a ocorrência de todas as possibilidades distintas de iluminação do painel, após seu acionamento?
Ajuda
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{ , com } n,r\in\mathbb{N} \text{ e } r\leqslant n[/tex].
Solução 1
Vamos determinar o total de possibilidades distintas de iluminação do painel no caso em que ficam duas seções na cor azul e uma na cor vermelha.
Assim, o total de possibilidades distintas de iluminação do painel, neste caso, é:
Agora, o cálculo do total de possibilidades distintas de iluminação do painel no caso em que ficam duas seções na cor vermelha e uma na cor azul, é idêntico ao do caso anterior. Portanto, o total de possibilidades distintas de iluminação do painel neste outro caso é [tex]252[/tex].
Logo, o total de possibilidades distintas de iluminação do painel é [tex]252+252 = 504[/tex].
Como cada uma dessas iluminações ocorre em [tex]1[/tex] segundo, o tempo gasto para ocorrerem todas essas possibilidades, considerando o melhor caso, isto é, aquele no qual as possibilidades não se repetem, é [tex]504[/tex] segundos. Mas veja que [tex]504 = 8\cdot 60+24[/tex]. Portanto, o tempo mínimo necessário para a ocorrência de todas as possibilidades distintas de iluminação do painel é de [tex]8[/tex] minutos e [tex]24[/tex] segundos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Poderíamos ter adotado uma estratégia diferente para contarmos o número de possibilidades distintas de iluminação do painel. Vejamos!
Vamos supor, inicialmente, que a cor diferente que irá acender esteja na seção localizada na primeira posição da primeira linha do painel (perceba que esta é uma das nove posições possíveis). Teremos, então, duas possibilidades: ou essa seção acende uma luz azul ou acende uma luz vermelha. Analisaremos as duas situações a seguir (observe que as duas análises são idênticas).
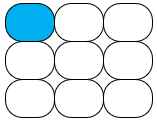 Nesta situação, as duas outras luzes que irão acender serão vermelhas. Então, queremos contar o número de pares possíveis de luzes vermelhas que poderão acender, fixando a luz acesa azul nesta posição.Como restam oito seções no painel, o total de modos de acenderem duas na cor vermelha é [tex]\qquad\begin{align}C_{8,2}&=\dfrac{8!}{2!\cdot (8-2)!}\\ &= \dfrac{8!}{2!\cdot 6!}=\dfrac{8\cdot 7}{2}=28\,.\end{align}[/tex] Então, fixada uma posição para acender a luz azul, duas luzes vermelhas poderão aparecer de [tex]28[/tex] maneiras distintas. Como podemos acender a luz azul em nove seções, e não apenas na primeira, o total de possibilidades distintas de iluminação do painel, neste caso, é [tex]9 \cdot 28= 252.[/tex] |
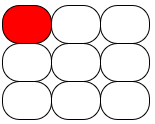 Nesta situação, as duas outras luzes que irão acender serão azuis. Então, queremos contar o número de pares possíveis de luzes azuis que poderão acender, fixando a luz acesa vermelha nesta posição.Como restam oito seções no painel, o total de modos de acenderem duas na cor azul é [tex]\qquad\begin{align}C_{8,2}&=\dfrac{8!}{2!\cdot (8-2)!}\\ &= \dfrac{8!}{2!\cdot 6!}=\dfrac{8\cdot 7}{2}=28\,.\end{align}[/tex] Então, fixada uma posição para acender a luz vermelha, duas luzes azuis poderão aparecer de [tex]28[/tex] maneiras distintas. Como podemos acender a luz vermelha em nove seções, e não apenas na primeira, o total de possibilidades distintas de iluminação do painel, neste caso, é [tex]9 \cdot 28= 252.[/tex] |
Portanto, o total de possibilidades distintas de iluminação do painel é [tex]\boxed{252+252=504}\,.[/tex]
Para finalizar essa segunda solução, precisamos calcular o tempo mínimo necessário para a ocorrência de todas essas [tex]504[/tex] possibilidades distintas de iluminação do painel. Para isso, observe que a cada segundo é aceso um dos [tex]504[/tex] conjuntos de três seções que calculamos. Logo, se um conjunto é aceso a cada segundo, será necessário, no mínimo, [tex]504[/tex] segundos, para que cada uma das possibilidades ocorra, sem repetição.
Mas, quantos minutos equivalem a [tex]504[/tex] segundos?
Como [tex]60[/tex] segundos equivale a [tex]1[/tex] minuto, para determinarmos quantos minutos cabem em [tex]504[/tex] segundos, basta fazer a divisão de [tex]504[/tex] por [tex]60[/tex]:
| [tex]\qquad \begin{array}{r} 504~\end{array} \begin{array}{|r} \,60\quad \\ \hline \end{array}[/tex] [tex]\qquad \begin{array}{r} \,\, \,24 \end{array}\begin{array}{r} \;\;\; 8~~~~~~~~~~~~~~~~ \end{array}[/tex] |
Assim, como [tex]504 = 8\cdot 60+24[/tex], então o tempo mínimo necessário para a ocorrência de todas as possibilidades distintas de iluminação do painel é de [tex]8[/tex] minutos e [tex]24[/tex] segundos. |
Solução elaborada pelos Moderadores do Blog.