✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
(UERJ 2013 – Adaptado) Dois terrenos, [tex]A[/tex] e [tex]B[/tex], ambos com a forma de trapézio, têm as frentes de mesmo comprimento voltadas para a Rua Alfa. Os fundos dos dois terrenos estão voltados para a Rua Beta. Observe o esquema:
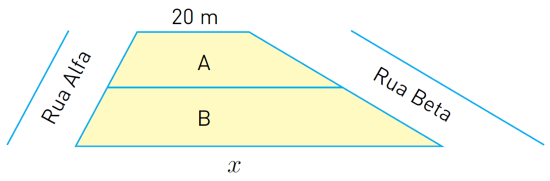
As áreas de [tex]A[/tex] e [tex]B[/tex] são, respectivamente, proporcionais a [tex]1[/tex] e [tex]2[/tex], e a lateral menor do terreno [tex]A[/tex] mede [tex]20 ~m[/tex].
Calcule o comprimento [tex]x[/tex], em metros, da lateral maior do terreno [tex]B[/tex].

Ajuda
(1) Para solucionar este problema será necessário utilizarmos um importantíssimo resultado da Geometria Plana atribuído a Tales de Mileto!
- Teorema de Tales: Se um feixe de retas paralelas, com no mínimo três retas, é intersectado por duas transversais, os segmentos de reta produzidos pelas paralelas sobre as transversais são proporcionais.
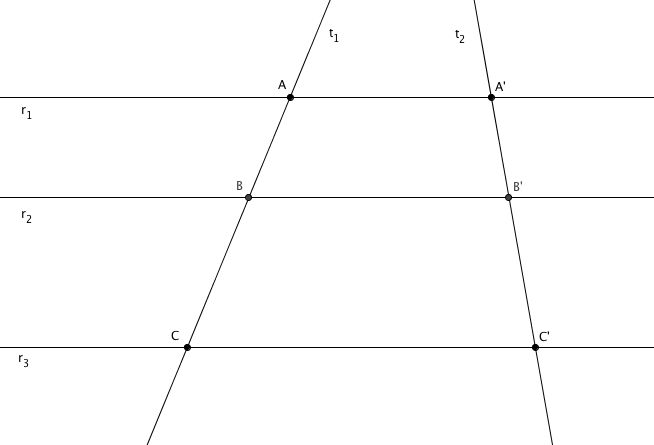
Por exemplo, se [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex] são retas paralelas e [tex]t_1[/tex] e [tex]t_2[/tex] são retas transversais a [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex], conforme mostra a figura a seguir, então[tex]\qquad \qquad \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}[/tex]
sendo que [tex]AB, \, BC, \, A’B’, \, B’C'[/tex] denotam, respectivamente, os comprimentos dos segmentos [tex]\overline{AB}, \, \overline{BC}, \, \overline{A’B’}, \, \overline{B’C’}[/tex].
(2) Vamos precisar, também, do tamanho da base média de um trapézio.
- Dado um trapézio qualquer, a sua base média é o segmento com extremos nos pontos médios dos seus dois lados não paralelos. Esse segmento é paralelo às duas bases do trapézio e a sua medida é igual à “média aritmética entre os comprimentos dessas duas bases”.
Solução
Duas observações iniciais.
Sejam [tex]h_1[/tex] e [tex]h_2[/tex] as alturas, em metros, dos trapézios [tex]A[/tex] e [tex]B[/tex], respectivamente, conforme figura abaixo.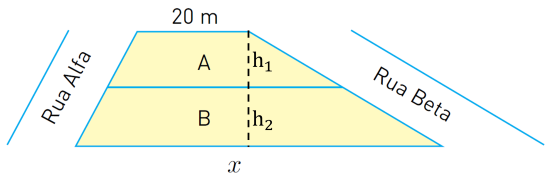 Como as frentes (voltadas para a Rua Alfa) dos terrenos [tex]A[/tex] e [tex]B[/tex] têm mesmo comprimento, digamos [tex]f[/tex] metros, pelo Teorema de Tales segue que: [tex]\qquad \dfrac{f}{h_1}= \dfrac{f}{h_2}\\ \qquad f \cdot h_2= f \cdot h_1\\ \qquad \bcancel{f} \cdot h_2= \bcancel{f} \cdot h_1\\ \qquad\boxed{h_1 = h_2}\,.[/tex] |
Ainda pelo fato de as frentes dos terrenos terem o mesmo comprimento, podemos aplicar uma vez mais o Teorema de Tales. Sejam, então, [tex]a[/tex] e [tex]b[/tex] os comprimentos em metros dos fundos dos dois terrenos [tex]A[/tex] e [tex]B[/tex], respectivamente.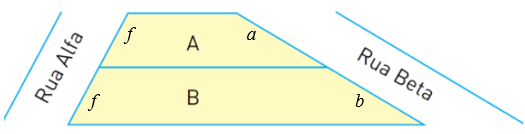 Assim, [tex]\qquad \dfrac{f}{a}= \dfrac{f}{b}\\ \qquad f \cdot b=f \cdot a\\ \qquad \bcancel{f} \cdot b=\bcancel{f} \cdot a\\ \qquad \boxed{a=b}\,.[/tex] |
Pelo exposto, além de as frentes dos terrenos terem o mesmo comprimento, os fundos dos terrenos também têm e, dessa forma, a linha que representa a divisão dos terrenos é a base média do trapézio maior (junção dos terrenos [tex]A[/tex] e [tex]B[/tex]), já que ela é definida pelos pontos médios dos lados não paralelos do trapézio. Portanto, o comprimento dessa linha é igual à média aritmética dos comprimentos das bases maior e menor do trapézio maior, ou seja, [tex]\dfrac{20+x}{2}[/tex].
Agora, calculando as áreas dos terrenos [tex]A[/tex] e [tex]B[/tex], temos
[tex]\qquad\text{Área (A)}=\dfrac{\left(\text{base maior + base menor}\right) \cdot \text{altura}}{2}\\
\qquad\text{Área (A)}=\dfrac{\left(\dfrac{20+x}{2}+20\right)\cdot h_1}{2}\\
\qquad\text{Área (A)}=\left(\dfrac{60+x}{2}\right)\cdot \dfrac{h_1}{2}\\
\qquad\boxed{\text{Área (A)}=\dfrac{(60+x)\cdot h_1}{4}};\\[/tex]
[tex]\qquad\text{Área (B)} = \dfrac{\left(\text{base maior + base menor}\right) \cdot \text{altura}}{2}\\
\qquad\text{Área (B)} = \dfrac{\left(x+ \dfrac{20+x}{2}\right)\cdot h_2}{2} \\
\qquad\text{Área (B)} =\left(\dfrac{20+3x}{2}\right)\cdot \dfrac{h_2}{2} \\
\qquad\boxed{\text{Área (B)} = \dfrac{(20+3x)\cdot h_1}{4}}.[/tex]
Como as áreas de [tex]A[/tex] e [tex]B[/tex] são, respectivamente, proporcionais a [tex]1[/tex] e [tex]2[/tex], segue que
[tex]\qquad\dfrac{\text{Área (A)}}{\text{Área (B)}}= \dfrac{1}{2} \\
\qquad\dfrac{\text{Área (A)}}{1}= \dfrac{\text{Área (B)}}{2} \\
\qquad\dfrac{\dfrac{(60+x)\cdot h_1}{4}}{1} = \dfrac{\dfrac{(20+3x)\cdot h_1}{4}}{2}\\
\qquad\dfrac{(60+x)\cdot \cancel{h_1}}{4} = \dfrac{(20+3x)\cdot \cancel{h_1}}{8}\\
\qquad\dfrac{(60+x)}{4} = \dfrac{(20+3x)}{8}\\
\qquad 8(60+x) = 4(20+3x)\\
\qquad 480+8x = 80+12x\\
\qquad 4x = 400\\
\qquad x = 100.[/tex]
Logo, [tex]x = 100~m.[/tex]
Solução elaborada pelos Moderadores do Blog.
Um vídeo para ajudar. . .
Assista ao vídeo abaixo para melhorar o seu entendimento e ampliar o seu conhecimento!
É só clicar na setinha.
