Problema
(Indicado a partir do 9º ano do E. F.)
O terreno mostrado na figura foi dividido em quatro terrenos menores por duas cercas retas. Estas cercas unem os pontos médios dos lados do terreno original. Em cada lote menor, o número que aparece indica a respectiva área em metros quadrados.
Qual é a área do lote destacado na figura?
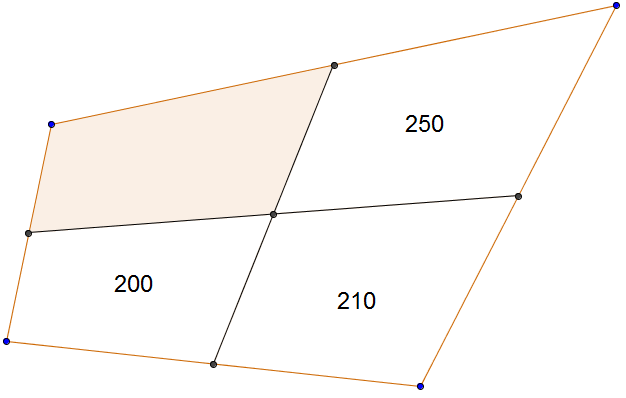
Adaptado da Segunda Fase da XXVII OLIMPÍADA BRASILEIRA DE MATEMÁTICA.
Solução
Ligando o ponto de interseção das retas que representam as duas cercas aos vértices, obtemos a seguinte figura:
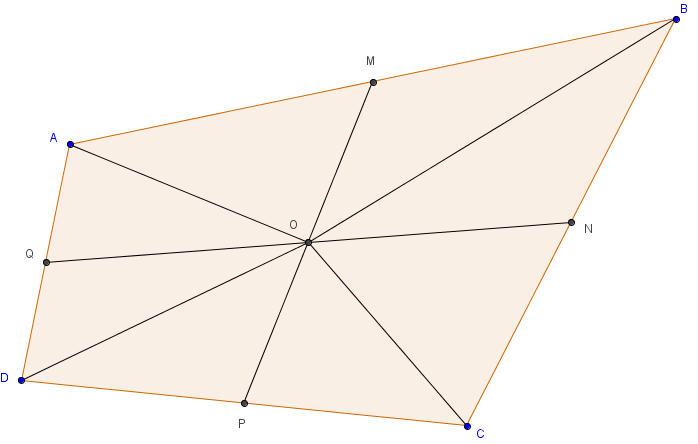
Observemos que, como os comprimentos dos segmentos AQ e QD são iguais e as alturas dos triângulos OAQ e OQD que passam por O são iguais, então as áreas de OAQ e OQD são iguais.
Analogamente, as áreas de “OAM e OMB”; “OBN e ONC”; “OCP e OPD” são iguais.
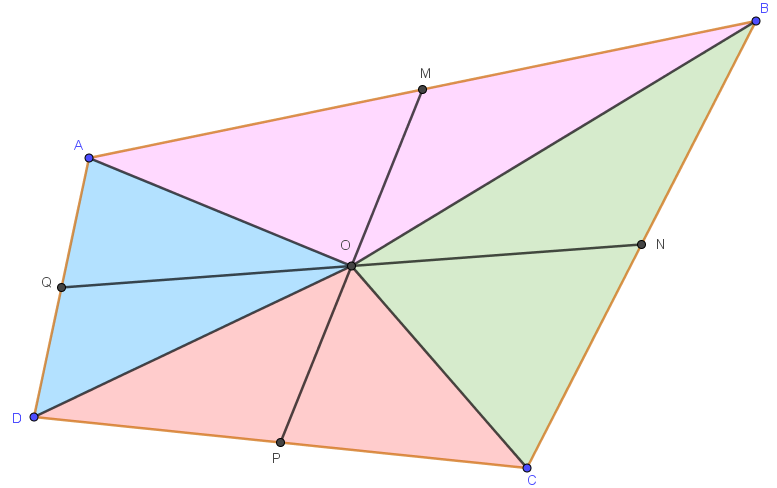
Assim:
área OAQ +área OAM + área OCP + área ONC =
= área OQD + área OMB + área OPD + área OBN,
donde segue que
área AMOQ + área CNOP = área DPOQ + área BMON
área AMOQ = área DPOQ + área BMON – área CNOP
área AMOQ = [tex]200+250-210=240[/tex]
e, portanto, a área requerida é 240 metros quadrados.
Solução elaborada pelos Moderadores do Blog.
