Problema- Perímetro de um triângulo
Problema
Dado um quadrado [tex]ABCD[/tex], escolhemos um ponto [tex]P[/tex], no lado [tex]\overline{CD}[/tex], e um ponto [tex]Q[/tex], no lado [tex]\overline{DA}[/tex], de modo que o ângulo determinado pelos segmentos [tex]\overline{BP}[/tex] e [tex]\overline{BQ}[/tex] meça [tex]45^\circ[/tex], conforme ilustra a figura a seguir.
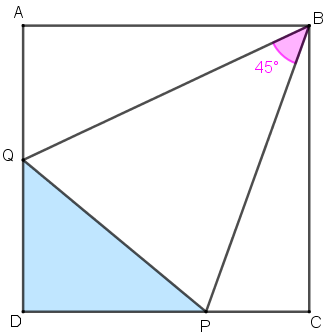
Se o comprimento de cada lado do quadrado [tex]ABCD[/tex] é [tex]x[/tex], qual é o perímetro do triângulo [tex]PDQ[/tex] em função de [tex]x[/tex]?
 |
Será que o applet abaixo não lhe ajuda a resolver o problema?
|
Um applet para ajudar
Instruções:
(1) Movimente os pontos [tex]\color{red}{P}[/tex] e [tex]\color{#7D7DFF}{Q}[/tex] até obter um ângulo [tex]Q\hat{B}P[/tex] de [tex]45^\circ[/tex], como previsto no problema. Definido esse ângulo, compare a sua resposta com a resposta do applet, observando que no applet construímos um quadrado com lados medindo [tex]x=5\,.[/tex]
(2) Para movimentar o ponto [tex]\color{red}{P}[/tex] (ou o ponto [tex]\color{#7D7DFF}{Q}[/tex]), basta clicar sobre ele com o botão esquerdo do mouse, manter o botão pressionado e fazer o movimento lentamente. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto [tex]\color{red}{P}[/tex] (ponto [tex]\color{#7D7DFF}{Q}[/tex]) e movimentá-lo horizontalmente (verticalmente).)
OBMEP_ srdg, criado com o GeoGebra
Dica: Você poderá fazer um movimento “mais fino” dos pontos [tex]\color{red}{P}[/tex] e [tex]\color{#7D7DFF}{Q}[/tex] utilizando seu teclado. Para isso:
- Clique sobre [tex]\color{red}{P}[/tex] com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para direita” e “mover para esquerda”.
- Clique sobre [tex]\color{#7D7DFF }{Q}[/tex] com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para cima” e “mover para baixo”.
 |
Para ver uma solução do problema, clique AQUI. |
Equipe COM – OBMEP
