Problema
(Indicado a partir do 9º ano do E. F.)
A figura mostra um triângulo equilátero dentro de um hexágono regular. Os lados do hexágono medem [tex]40 \text{ cm}[/tex] e os vértices do triângulo são pontos médios de três lados do hexágono.
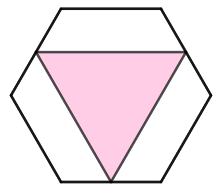
Quanto vale o perímetro do triângulo?
Adaptado de UK Junior Mathematical Olympiad, 2015.
Solução
A partir do seu centro, todo hexágono regular pode ser decomposto em seis triângulos equiláteros congruentes cujo comprimento dos lados é o comprimento dos lados do próprio hexágono, conforme podemos visualizar no gif animado mostrado abaixo.
OBMEP_srg, criado com o GeoGebra
Então, partindo dos pontos médios de seus lados, podemos dividir cada um desses triângulos em quatro pequenos triângulos equiláteros. (Esse é um resultado bastante intuitivo, mas, para uma justificativa formal, você pode consultar a parte inicial da solução desta questão:
http://clubes.obmep.org.br/blog/problema-para-ajudar-na-escola-porcentagem-da-area/).
Logo, em particular, o hexágono do problema pode ser dividido em [tex]24[/tex] pequenos triângulos equiláteros, conforme mostrado abaixo.
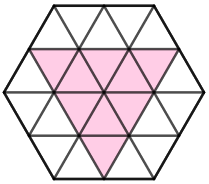
Com isso, cada um desses pequenos triângulos tem lados medindo [tex]40\div 2=20 \text{ cm}[/tex] e, portanto, cada lado do triângulo colorido mede [tex]3\times 20=60\text{ cm}[/tex]. Assim, seu perímetro é de [tex]3\times 60=\, \fcolorbox{black}{#eee0e5}{$180 \text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
