Problema
(Indicado a partir do 9º ano do E. F.)
Um fazendeiro possui um terreno no formato de um triângulo equilátero e nesse terreno tem um porco amarrado em um dos vértices. Os lados do terreno medem [tex]100 \text{ m}[/tex] e a porção do terreno a que o porco tem acesso corresponde à metade da área do triângulo.
Deste modo, qual é o comprimento da corda que prende o porco?
Para seus cálculos, desconsidere o tamanho do porco.
Adaptado do Almanaque das Curiosidades Matemáticas, Ian Stewart.

Lembrete
Um triângulo equilátero de lado medindo [tex]l\text{ m}[/tex] tem área dada por:
[tex]\qquad A = \dfrac{l^2\sqrt{3}}{4}\text{ m}^2.[/tex]
Solução
Observe que:
- Como a medida do lado do terreno é [tex]100\;m[/tex], então a área desse terreno é dada por:
- A área de acesso do porco deve ser igual à metade da área do terreno, ou seja,
- O terreno tem o formato de um triângulo equilátero; assim, os seus ângulos internos medem [tex]60^\circ[/tex].
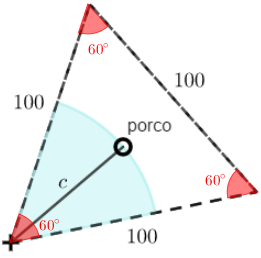
Com isso, a área de acesso do porco corresponde a um setor circular de [tex]60^{\circ}[/tex], cujo raio é igual ao comprimento da corda à qual o porco está amarrado. Sendo [tex]c[/tex] o comprimento dessa corda em metros, temos a situação ilustrada na figura a seguir.
[tex]\quad A=\dfrac{100^2\sqrt{3}}{4}\\
\quad A=\dfrac{\left(2\cdot 50 \right)^2\sqrt{3}}{4}\\
\quad A=\dfrac{\left(2\right)^2 \cdot \left(50 \right)^2\sqrt{3}}{4}\\
\quad A=\dfrac{\cancel{4} \cdot50^2\sqrt{3}}{\cancel{4}} \\
\quad A=50^2\sqrt{3} \text{ m}^2.[/tex]
[tex]\quad A_p=\dfrac{50^2\sqrt{3}}{2}\\
\quad A_p=1250\sqrt{3}\text{ m}^2\,.\qquad \textcolor{#800000}{(i)}[/tex]
Assim, temos que a área de acesso do porco corresponde a [tex]\dfrac{1}{6}[/tex] da área do círculo de raio [tex]c[/tex], ou seja, [tex]\dfrac{1}{6}\pi c^2.\qquad \textcolor{#800000}{(ii)}[/tex]
Igualando [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\,\\
\qquad \dfrac{1}{6}\pi c^2 = 1250\sqrt{3}\\
\qquad \pi c^2 = 6\times 1250\sqrt{3}\\
\qquad \pi c^2 = 7500\sqrt{3}\\
\qquad c^2 = \dfrac{7500\sqrt{3}}{\pi}\\
\qquad c = \sqrt{\dfrac{7500\sqrt{3}}{\pi}}\quad (c \gt 0)\\
\qquad c =\dfrac{ \sqrt{7500\sqrt{3}}} {\sqrt{\pi}}\quad \\
\qquad c =\dfrac{ \sqrt{(2500 \cdot 3)\sqrt{3}}} {\sqrt{\pi}}\quad \\
\qquad c =\dfrac{ \sqrt{2500}\sqrt{3\sqrt{3}}} {\sqrt{\pi}}\quad \\
\qquad c = \dfrac{50\sqrt{3\sqrt{3}}}{\sqrt{\pi}}\\
\qquad c = 50\sqrt{\dfrac{3\sqrt{3}}{\pi}}.[/tex]
Portanto, o comprimento da corda é de [tex]\fcolorbox{black}{#eee0e5}{$50\sqrt{\dfrac{3\sqrt{3}}{\pi}}\text{ m}$}\,[/tex], aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$64,3\text{ m}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
