Problema
(Indicado a partir do 9º ano do E. F.)
O pequeno e desconhecido vilarejo alpino Après-le-Ski situa-se em um vale profundo, cercado de penhascos verticais em ambos os lados. Os penhascos têm [tex]600 \text{ m}[/tex] de altura de um lado e [tex]400 \text{ m}[/tex] do outro. Teleféricos correm da base de cada penhasco para o topo do penhasco oposto.
Um observador fez um desenho em duas dimensões da situação descrita, supondo que os cabos por onde os teleféricos correm são perfeitamente retos.
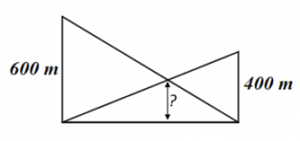
Nesse desenho, qual a altura do suposto ponto de cruzamento dos cabos?
Adaptado do Almanaque das Curiosidades Matemáticas, Ian Stewart.
Solução
No desenho feito pelo observador, tracemos um segmento para representar a altura que procuramos, conforme figura abaixo.
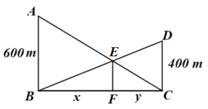
- Note que os triângulos [tex]ABC[/tex] e [tex]EFC[/tex] são semelhantes pelo Caso A.A. (Não se lembra desse caso de semelhança? Então visite esta Sala do Blog.).
- Veja ainda que os triângulos [tex]BCD[/tex] e [tex]BFE[/tex] também são semelhantes pelo mesmo caso. Assim,
Assim:
[tex]\qquad \dfrac{EF}{AB} = \dfrac{FC}{BC}\\
\qquad \dfrac{EF}{600} = \dfrac{y}{x+y}.\qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad \dfrac{EF}{CD} = \dfrac{BF}{BC}\\
\qquad \dfrac{EF}{400} = \dfrac{x}{x+y}.\qquad \textcolor{#800000}{(ii)} [/tex]
Somando as equações [tex]\textcolor{#800000}{(i)}\,[/tex] e [tex]\,\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad \dfrac{EF}{600}+\dfrac{EF}{400} = \dfrac{y}{x+y}+\dfrac{x}{x+y}\\
\qquad \dfrac{EF}{600}+\dfrac{EF}{400} = \dfrac{x+y}{x+y} = 1\\
\qquad \dfrac{2EF+3EF}{1200}= 1\\
\qquad \dfrac{5EF}{1200}= 1\\
\qquad 5EF = 1200\\
\qquad EF = 240\;m.[/tex]
Portanto, o suposto ponto de cruzamento dos cabos está a uma altura de [tex]\, \fcolorbox{black}{#eee0e5}{$240 \text{ m} $}\,[/tex] do solo.
Solução elaborada pelos Moderadores do Blog.
