Problema
(Indicado a partir do 9º ano do E. F.)
Na figura abaixo, [tex]ABCD[/tex] representa um quadrado e o segmento [tex]\overline{AP}[/tex], quando prolongado, faz um ângulo de [tex]90^\circ[/tex] com o segmento [tex]\overline{CQ}[/tex] no ponto [tex]G[/tex].
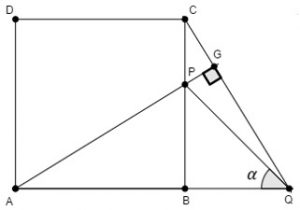
Calcule a medida do ângulo [tex]P\hat Q B[/tex].
Extraído do PAPMEM – IMPA.

Lembretes e notações
(I) As três alturas de um triângulo se intersectam em um ponto denominado ortocentro.
(II) A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ.[/tex]
(III) Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex].
(IV) Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y. [/tex]
Solução
Inicialmente, vamos construir a diagonal [tex]\overline{AC}[/tex] do quadrado [tex]ABCD[/tex] e destacar o ângulo reto no vértice [tex]B[/tex]. Perceba que a medida do ângulo [tex]C\widehat{A} B[/tex] é [tex]45^\circ[/tex], pois a diagonal do quadrado é também bissetriz.
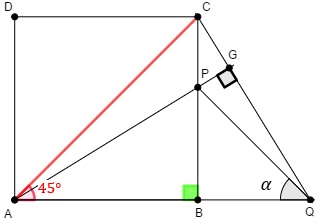
Note que [tex]\overline{CB}[/tex] e [tex]\overline{AG}[/tex] são alturas do triângulo [tex]ACQ[/tex]. Logo, pelo Lembrete I, o ponto [tex]P[/tex] é o ortocentro do triângulo [tex]ACQ[/tex]. Assim, o prolongamento do segmento [tex]\overline{PQ}[/tex] intercepta a diagonal [tex]\overline{AC}[/tex] em um ponto [tex]J[/tex] de tal forma que [tex]\overline{QJ}[/tex] é também uma altura do triângulo [tex]ACQ[/tex] e, portanto, o ângulo [tex]A\hat J Q[/tex] mede [tex]90^\circ\,.[/tex]
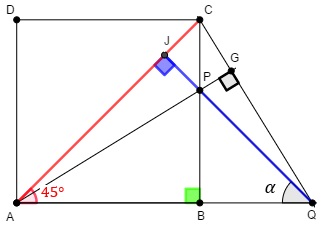
Dessa forma, pelo Lembrete II, no triângulo [tex]AJQ[/tex] temos:
[tex]\qquad 45^\circ + 90^\circ + \alpha = 180^\circ\\
\qquad \alpha = 45^\circ.[/tex]
Então, a medida do ângulo [tex]P\hat Q B[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$ 45^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
