Problema
(Indicado a partir do 1º ano do E. M.)
Um tanque é abastecido por uma torneira e o volume de água em seu interior, em milhares de litros, é dado por [tex]V_{1}(t)=3t+13[/tex], com [tex]t[/tex] contado em horas a partir do instante [tex]t=0[/tex] em que a torneira é aberta. No instante [tex]t_{1}[/tex] em que o volume de água atinge a capacidade máxima do tanque, a torneira é automaticamente fechada e, imediatamente, um registro é aberto permitindo que a água acumulada nesse tanque abasteça caixas d’água menores. A partir do momento em que esse registro é aberto, o volume d’água no tanque passa a ser descrito pela função [tex]V_{2}(t)=-2t+58[/tex], para [tex]t \geq t_{1}[/tex], até que o tanque esteja completamente vazio.
Calcule a capacidade máxima do tanque e em quanto tempo o tanque estará vazio depois de fechada a torneira e aberto o registro.
Extraído do PISM -UFJF – Programa de Ingresso Seletivo Misto.
Solução
Inicialmente, vamos esboçar os gráficos das funções [tex]V_{1}[/tex] (azul) e [tex]V_{2}[/tex] (vermelho), em um mesmo plano cartesiano [tex]xOy[/tex]. Deixamos contínuo o intervalo no qual os gráficos se aplicam à situação problema.
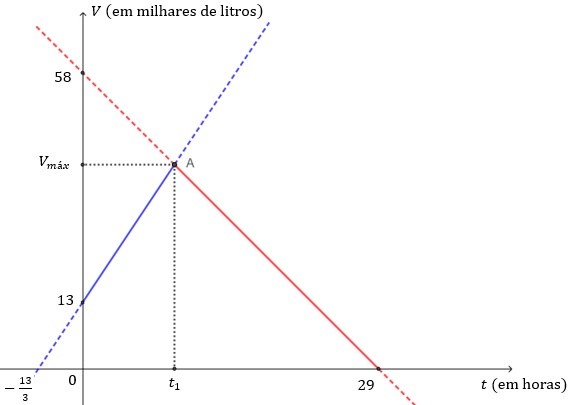
Note que as duas retas se intersectam no ponto [tex]A[/tex]. (Esse ponto representa o fechamento da torneira e a abertura do registro.)
Assim, a abscissa de [tex]A[/tex] é o número real [tex]t_1[/tex] tal que [tex]V_1(t_1)=V_2(t_1)[/tex]; vamos calculá-la:
[tex]\qquad V_1(t_1)=V_2(t_1)\\
\qquad 3t_1+13=-2t_1+58\\
\qquad5t_1=45\\
\qquad t_{1}=9.[/tex]
Analise com cuidado o gráfico acima e perceba que a capacidade máxima do tanque, denotada por [tex]V_{máx}[/tex], é a ordenada do ponto [tex]A[/tex]; vamos calculá-la, também:
[tex]\qquad V_{máx}=V_{1}(9)=3\cdot 9 +13[/tex]
[tex]\qquad V_{máx}=40[/tex].
Portanto, a capacidade máxima do tanque é de [tex]\fcolorbox{black}{#eee0e5}{$40000 \text{ litros}$}[/tex] e, como a função [tex]V_{2}[/tex] possui zero em [tex]t=29[/tex], o tempo em que o tanque estará vazio depois de fechada a torneira e aberto o registro é [tex]\fcolorbox{black}{#eee0e5}{$29-9=20 \text{ horas}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
AJUDA
 |
Se você se atrapalhou com as denominações abscissa e ordenada, talvez o vídeo abaixo possa ajudar!
|
Referencial Cartesiano (Abcissas e ordenadas)
