✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F.- Nível de dificuldade: Difícil)
Utilizando seis triângulos equiláteros, foi montada a figura abaixo.
Os lados dos triângulos medem o dobro dos lados do hexágono regular central; então, que fração da área total dos seis triângulos corresponde à área do hexágono?

Adaptado da XIV ONM, 2014.
Solução
- Em problemas desse tipo, muitas vezes é útil tentar decompor a figura inicial em outras figuras menores todas iguais entre si.
Particularmente, prolongando alguns segmentos da figura original, conseguimos decompô-la em triângulos equiláteros congruentes (iguais), conforme mostra a figura a seguir.
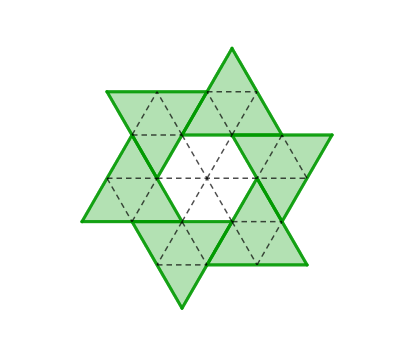
Assim, cada um dos seis triângulos originais ficou dividido em quatro triângulos equiláteros pequenos e o hexágono central ficou dividido em seis pequenos triângulos. Dessa forma,
- os seis triângulos iniciais que definiram a figura contêm [tex]6 \times 4=24[/tex] triângulos pequenos;
- o hexágono central contém [tex]6 [/tex] triângulos pequenos;
donde concluímos que a área do hexágono corresponde a [tex]\fcolorbox{black}{#adebb7}{$\dfrac{6}{24}=\dfrac{1}{4}$}[/tex] da área total dos seis triângulos.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
