Problema
(Indicado a partir do 7º ano do E. F.)
O diagrama abaixo mostra sete círculos e cada uma das três setas indica uma "linha de três círculos". Os dígitos de 1 a 7 devem ser colocados nos círculos, um por círculo, de modo que a soma dos dígitos em cada uma das três "linhas de três círculos" indicadas seja a mesma.
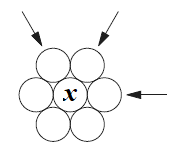
Encontre todos os valores possíveis de [tex]x[/tex].
Extraído da Olympiad Cayley.
Solução
Preenchemos o restante dos círculos com as letras [tex]a, b, c, d, e[/tex] e [tex]f[/tex], como mostra a figura abaixo.
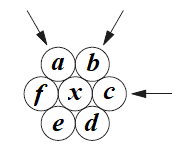
Claramente a soma dos números em todos os círculos é igual à soma dos números de 1 a 7, ou seja, [tex]a+b+c+d+e+f+x = 28[/tex].
Seja [tex]S[/tex] a soma em cada uma das três linhas. Então:
\begin{align}
a+x+d &= S\\
b+x+e &= S\\
c+x+f &= S.
\end{align}
Somando as três equações acima, obtemos
\begin{align}
(a+x+d)+(b+x+e)+(c+x+f ) &= 3S\\
(a+b+c+d+e+f+x)+2x &= 3S\\
28+2x &= 3S\\
27+(2x+1) &= 3S.
\end{align}
Como [tex]3S[/tex] e [tex]27[/tex] são múltiplos de [tex]3[/tex], então [tex](2x+1)[/tex] também deve ser.
Logo, os possíveis valores para [tex]x[/tex] são [tex]\, \fcolorbox{black}{#eee0e5}{$x =1$}\,[/tex], [tex]\, \fcolorbox{black}{#eee0e5}{$x= 4$}\,[/tex] ou [tex]\, \fcolorbox{black}{#eee0e5}{$x = 7$}\,.[/tex]
A seguir apresentamos três possíveis distribuições dos números nos círculos.
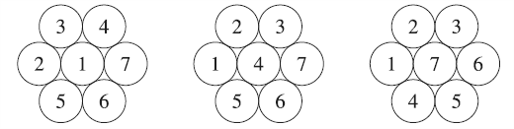
Solução elaborada pelos Moderadores do Blog.
