Problema
(A partir do 8º ano do E. F.- Nível de dificuldade: Difícil)
A partir de cinco segmentos de reta foi traçada a figura a seguir, na qual vemos cinco ângulos com a mesma medida [tex]\theta[/tex].
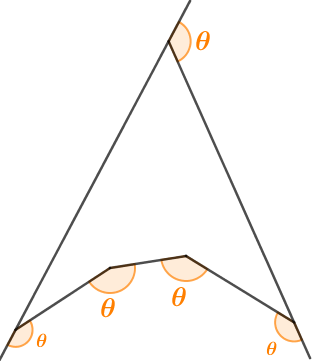
Determine [tex]\theta[/tex], em graus.

Lembretes
✐ A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ.[/tex]
✐ A soma das medidas dos ângulos internos de qualquer pentágono é [tex]540^\circ.[/tex]
Solução
Inicialmente, observamos que você pode ter estranhado o lembrete que afirma que "a soma das medidas dos ângulos internos de qualquer pentágono é [tex]540^\circ[/tex]". Mas essa informação vale até mesmo para pentágonos como o do problema, que não é regular e nem convexo. (Lembre-se de que se um polígono não é convexo, com mais razão não será regular.)
Observe na figura seguinte que, mesmo não sendo regular e nem convexo, podemos dividir o pentágono do problema internamente em três triângulos cujas somas das medidas dos ângulos internos definem a soma das medidas dos ângulos internos do pentágono [tex](3 \times 180^\circ=540^\circ)\,.[/tex]
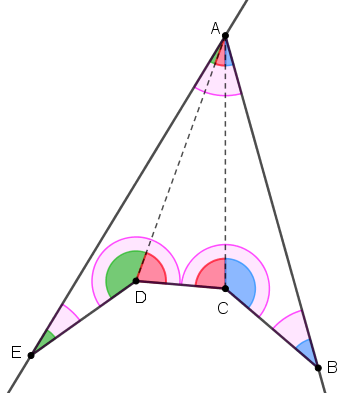
Vamos à solução do problema.
Observe que as cinco medidas [tex]\theta[/tex] definem as medidas dos cinco ângulos internos do pentágono.
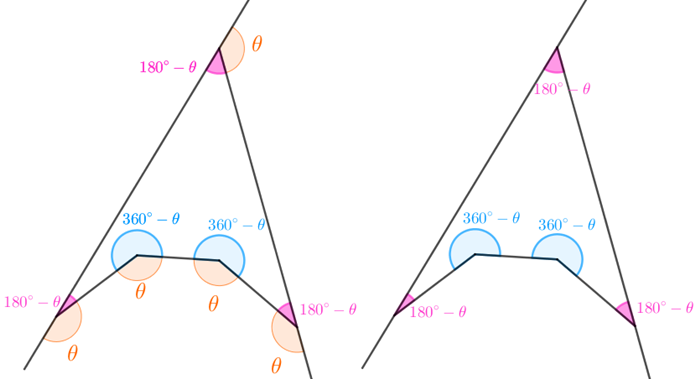
Portanto, temos que
[tex]\qquad 3\cdot\left(180^\circ-\theta\right)+2\cdot\left(360^\circ-\theta\right)=540^\circ\\
\qquad 540^\circ-3\theta+720^\circ-2\theta=540^\circ\\
\qquad 720^\circ=5\theta\\
\qquad \fcolorbox{black}{#eee0e5}{$\theta=144^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
