Problema
(A partir da 6ª série do E. F.- Nível de dificuldade: Médio)
Ao sair de casa para uma breve viagem, Soemi observou que o marcador de combustível de seu carro indicava que no tanque ainda tinha a quantidade de combustível que pode ser visualizada na figura a seguir (área colorida).
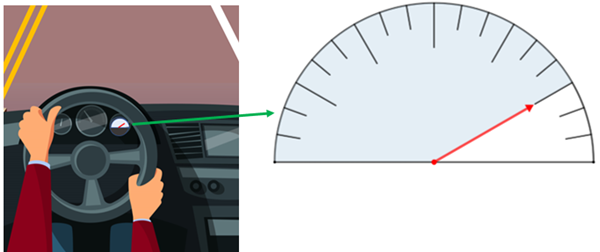Imagem do volante extraída de Freepik
Ao chegar da viagem, Soemi percebeu que o carro consumiu [tex]2/3[/tex] do combustível que estava no tanque quando ela saiu.
(a) Leia no desenho acima a fração da capacidade total do tanque do carro de Soemi que corresponde à quantidade de combustível de quando ela saiu.
(b) Reproduza o desenho abaixo e marque a localização do ponteiro marcador quando da chegada de Soemi.
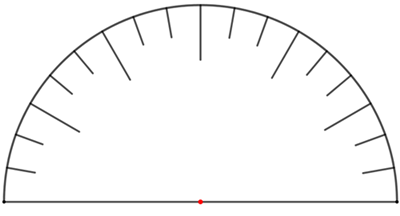
(c) No desenho que você completou, leia a fração da capacidade total do tanque que corresponde ao combustível consumido na viagem.
(d) A fração que você encontrou em (c) corresponde ao produto de que frações envolvidas no problema?
Observação: Você pode utilizar o applet abaixo para o item (b) .
Solução
(a) Observe que os segmentos mais longos dividem o marcador de combustível em seis partes iguais, das quais cinco correspondem à quantidade de combustível no tanque do carro.
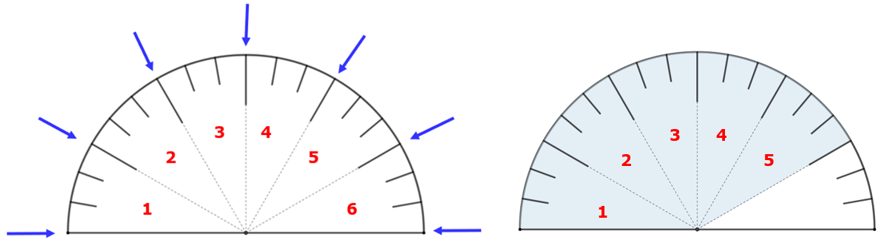
Assim, considerando que a área azul mostra a quantidade de combustível no tanque, a fração da capacidade total do tanque do carro de Soemi que corresponde à quantidade de combustível de quando ela saiu é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{5}{6}$}[/tex] (cinco sextos).
(b) Observe que as cinco partes que correspondem à quantidade de combustível no tanque do carro na saída da Soemi não é um parâmetro confortável para resolvermos este item, uma vez que [tex]5[/tex], que agora corresponde ao nosso todo, não é divisível por [tex]3[/tex], que é o número de partes iguais que devemos dividir o nosso todo. Vamos, então, considerar todas as [tex]15[/tex] marcações que dividem a área azul da figura em partes iguais. Para facilitar ainda mais a nossa solução, vamos agrupar as quinze divisões de cinco em cinco. (Observe que numeramos as regiões no sentido anti-horário, pois vamos considerar o consumo e, portanto, a retirada de combustível.)
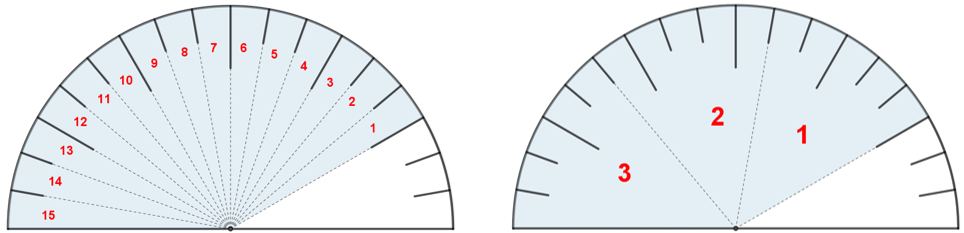
Como o carro de Soemi consumiu [tex]2/3[/tex] do combustível que estava no tanque quando ela saiu, a marcação do ponteiro quando da chegada dela é mostrada na figura a seguir.
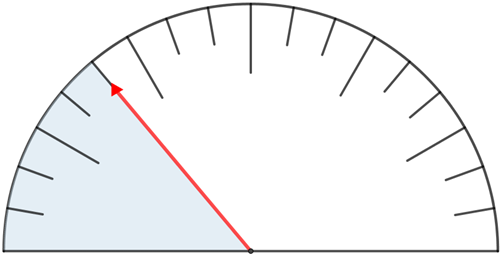
Observe que a área colorida corresponde ao que restou de combustível no tanque do carro, após a viagem, [tex]1/3[/tex] do combustível que estava no tanque.
(c) Vamos fazer a leitura da fração que corresponde ao combustível consumido na viagem, mas com relação à capacidade total do tanque. Então, neste item, o "todo" é a capacidade do tanque e a "parte" é a quantidade de combustível consumido na viagem.
Vamos, agora, considerar todas as [tex]18[/tex] marcações que dividem em partes iguais a figura que representa o tanque de combustível do carro da Soemi.
Pelo item (b), podemos concluir que o combustível consumido na viagem corresponde a [tex]10[/tex] das [tex]18[/tex] marcações que utilizamos para dividir em partes iguais o nosso todo.
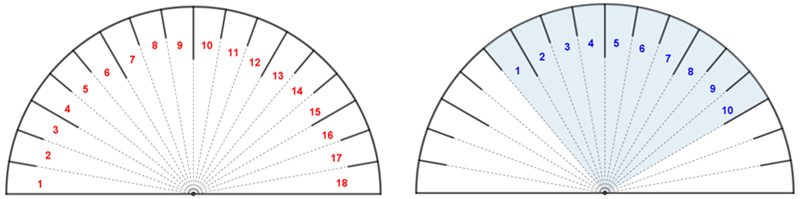
Assim, a fração da capacidade total do tanque do carro que corresponde à quantidade do combustível consumido na viagem da Soemi é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{10}{18}=\dfrac{5}{9}$}\,.[/tex]
Poderíamos ter obtido diretamente a fração [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{5}{9}$}\,[/tex],(cinco nonos), se tivéssemos considerado o todo dividido em nove partes iguais. Veja a próxima figura.
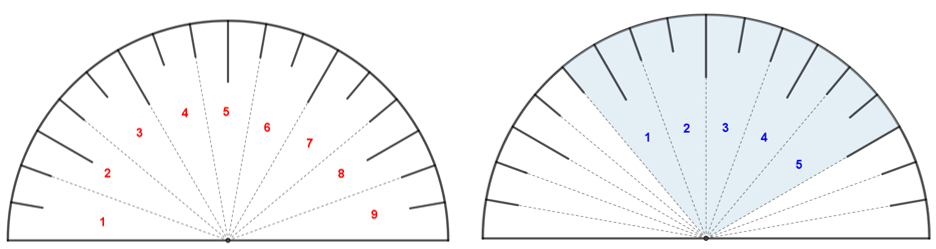
(d) Observe que a fração encontrada no item (c) corresponde ao produto das frações [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{2}{3}$}\,[/tex] e [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{5}{6}$}\,[/tex], observe:
[tex]\qquad \dfrac{2}{3} \times \dfrac{5}{6}=\dfrac{10}{18}=\dfrac{5}{9}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |