.Problema para ajudar na escola: Zigue-zague

Problema
(A partir da 7ª série do E. F.- Nível de dificuldade: Difícil)

---

Na figura abaixo, vemos oito quadradinhos de lados [tex]1\text{ cm}[/tex] em zigue-zague. O perímetro da figura é [tex]18\text{ cm}\,.[/tex]

Qual o perímetro de um zigue-zague construído da mesma forma, só que com 2020 quadradinhos?

Solução

---

Vamos iniciar a análise do zigue-zague observando um bloco com dois quadradinhos.
Sabemos que o perímetro de uma figura é a soma das medidas de todos os lados dessa figura. Por sua vez, de maneira informal, os lados são as partes que limitam a figura. Assim, conforme indica a imagem a seguir, o perímetro de um bloco isolado do zigue-zague é [tex]6\text{ cm}\,.[/tex]

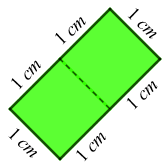
Observe que o segmento que aparece tracejado na imagem não compõe o perímetro do bloco, uma vez que esse segmento não limita o bloco, apenas divide-o internamente.
Vamos observar agora dois blocos consecutivos da figura.

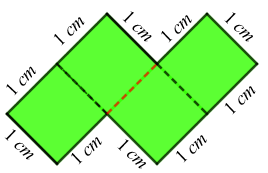
Isolado, cada bloco tem perímetro igual a [tex]6\text{ cm}[/tex]; mas quando pegamos dois blocos para formar um bloco maior com quatro quadradinhos, "perdemos dois lados" do perímetro e o bloco maior fica com perímetro igual a [tex]6+6-2=10\text{ cm}\,.[/tex]
Com isso, cada novo bloco com dois quadradinhos que agregamos à figura acrescentará [tex]4\text{ cm}[/tex] ao perímetro da figura (lembre-se de que perderemos dois lados por cada bloco agregado).
Dessa forma, a figura do problema tem realmente perímetro igual a [tex]18\text{ cm}\,.[/tex] Observe:

• [tex]1[/tex] bloco: [tex]1\times 2=2[/tex] quadradinhos → Perímetro [tex]=6\text{ cm}\,.[/tex]
• [tex]2[/tex] blocos: [tex]2\times 2=4[/tex] quadradinhos → Perímetro [tex]=6+4=10\text{ cm}\,.[/tex]
• [tex]3[/tex] blocos: [tex]3\times 2=6[/tex] quadradinhos → Perímetro [tex]=6+4+4=14\text{ cm}\,.[/tex]
• [tex]4[/tex] blocos: [tex]4\times 2=8[/tex] quadradinhos → Perímetro [tex]=6+4+4+4=18\text{ cm}\,.[/tex]

Para um zigue-zague construído com [tex] 2020[/tex] quadradinhos, precisaremos de [tex] 2020 \div 2=1010[/tex] blocos. Assim, continuando a listagem acima:

• [tex]1[/tex] bloco: [tex]1\times 2=2[/tex] quadradinhos → Perímetro [tex]=6\text{ cm}\,.[/tex]
• [tex]2[/tex] blocos: [tex]2\times 2=4[/tex] quadradinhos → Perímetro [tex]=6+4=10\text{ cm}\,.[/tex]
• [tex]3[/tex] blocos: [tex]3\times 2=6[/tex] quadradinhos → Perímetro [tex]=6+4+4=14\text{ cm}\,.[/tex]
• [tex]4[/tex] blocos: [tex]4\times 2=8[/tex] quadradinhos → Perímetro [tex]=6+4+4+4=18\text{ cm}\,.[/tex]

[tex]\vdots[/tex]

• [tex]1010[/tex] blocos: [tex]1010\times 2=2020[/tex] quadradinhos → Perímetro [tex]=6+\underbrace{4+4+\cdots+4}_{1009\text{ vezes}}=\textcolor{red}{?}\text{ cm}\,.[/tex]

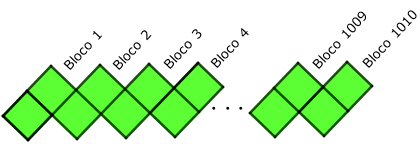
Então, para responder à pergunta

► Qual o perímetro de um zigue-zague construído da mesma forma, só que com 2020 quadradinhos?

só precisamos calcular a soma [tex]S=6+\underbrace{4+4+\cdots+4}_{1009\text{ vezes}}\,.[/tex]
Vamos lá:
[tex]\qquad S=6+\underbrace{4+4+\cdots+4}_{1009\text{ vezes}}\\
\qquad S=6+1009 \times 4\\
\qquad S=6+4036\\
\qquad S=4042\\
[/tex]
Portanto, o perímetro de um zigue-zague construído com [tex]2020[/tex] quadradinhos é [tex]\,\fcolorbox{black}{#eee0e5}{$4042 \text{ cm}$}\,.[/tex]

---

Solução elaborada pelos Moderadores do Blog.