Problema
(Indicado a partir do 1º ano do E. M.)
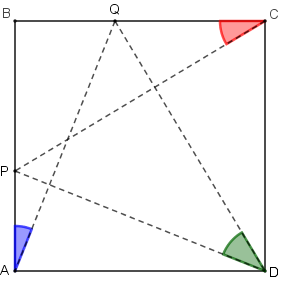
Nicholas marcou os pontos [tex]P[/tex] e [tex]Q[/tex] sobre os lados de um quadrado [tex]ABCD[/tex], como indica a figura abaixo, de modo que a soma dos comprimentos dos segmentos [tex]\overline{PB}[/tex] e [tex]\overline{BQ}[/tex] fosse igual ao comprimento do lado do quadrado [tex]ABCD[/tex].
Tendo feito as marcações, Nicholas observou que a soma das medidas dos ângulos [tex]Q\widehat{A} P[/tex], [tex]Q\widehat{C}P[/tex] e [tex]Q\widehat{D}P[/tex] resultava em um valor notável.
Você sabe dizer qual o valor dessa soma, sem fazer qualquer medição? Justifique sua resposta.

Notações
(I) Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
(II) Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y [/tex] e sua respectiva medida por [tex]mX\widehat{V}Y.[/tex]
Solução
Observe que:
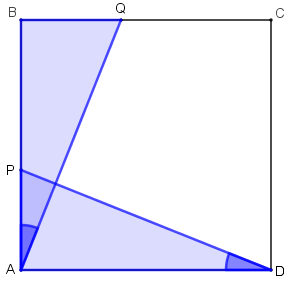
- A soma dos comprimentos dos segmentos [tex]\overline{PB}[/tex] e [tex]\overline{BQ}[/tex] é igual ao comprimento do lado do quadrado [tex]ABCD[/tex]. Assim, [tex]PB+BQ=AP+PB[/tex], donde [tex]BQ=AP[/tex]. Assim, os triângulos [tex]BAQ [/tex] e [tex]ADP [/tex] são congruentes (caso L.A.L.) e, portanto, o ângulo [tex]Q\widehat{A}P [/tex] é congruente ao ângulo [tex]\textcolor{#0000FF}{P\widehat{D}A} [/tex].
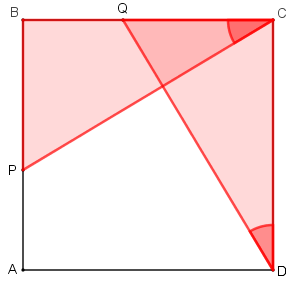
- Como a soma dos comprimentos dos segmentos [tex]\overline{PB}[/tex] e [tex]\overline{BQ}[/tex] é igual ao comprimento do lado do quadrado [tex]ABCD[/tex], então [tex]PB+BQ=BQ+QC[/tex], donde [tex]PB=QC.[/tex] Dessa forma, temos que os triângulos [tex]PBC[/tex] e [tex]QCD[/tex] também são congruentes (caso L.A.L.) e, consequentemente, o ângulo [tex]\textcolor{#FF0000}{Q\widehat{C}P} [/tex] é congruente ao ângulo [tex]\textcolor{#FF0000}{C\widehat{D}Q}.[/tex]
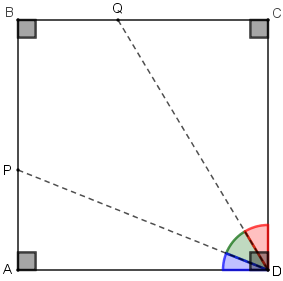
- Sabemos que a soma dos ângulos [tex]\textcolor{#FF0000}{C\widehat{D}Q}[/tex], [tex]\textcolor{#339900}{Q\widehat{D}P}[/tex] e [tex]\textcolor{#0000FF}{P\widehat{D}A} [/tex] é o ângulo reto [tex]C\widehat{D}A[/tex], pois [tex]ABCD [/tex] é um quadrado.
Pelo exposto,
[tex]\qquad \begin{align*}\textcolor{#0000FF}{mQ\widehat{A}P}+\textcolor{#FF0000}{mQ\widehat{C}P}+\textcolor{#339900}{mQ\widehat{D}P}&=\textcolor{#FF0000}{mQ\widehat{C}P}+\textcolor{#339900}{mQ\widehat{D}P}+\textcolor{#0000FF}{mQ\widehat{A}P}\\
&=\textcolor{#FF0000}{mC\widehat{D}Q}+\textcolor{#339900}{mQ\widehat{D}P}+\textcolor{#0000FF}{mP\widehat{D}A}\\
&={mC\widehat{D}A}=90^\circ .\end{align*}[/tex]
Logo, a soma das medidas dos três ângulos em questão é igual a [tex]90^\circ[/tex].
Solução elaborada pelo Clube Eureka!, com contribuições dos Moderadores do Blog .
