Problema
(Indicado a partir do 9º ano do E. F.)
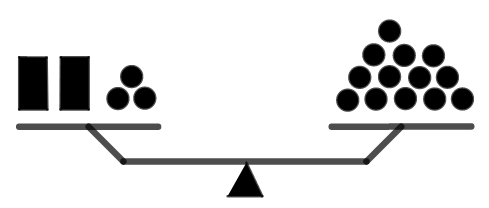
Dois paralelepípedos idênticos e dezesseis esferas idênticas equilibram uma balança de dois pratos, como mostra a figura.
Quantas esferas são necessárias para equilibrar apenas um dos paralelepípedos?
Solução 1
- Como as esferas possuem a mesma massa, pois são idênticas, e a balança está inicialmente equilibrada, podemos remover três esferas de cada um dos pratos desta balança sem desequilibrá-la. Como resultado teremos apenas os dois paralelepípedos em um dos pratos e dez esferas no outro.
- Agora removeremos a metade da massa existente em cada um dos pratos e o resultado será apenas um paralelepípedo em um dos pratos e cinco esferas no outro.
Portanto, são necessárias [tex]\,\fcolorbox{black}{#eee0e5}{$\text{cinco}$} [/tex] esferas para equilibrar um paralelepípedo.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sejam [tex]\textcolor{blue}{b\,}[/tex] e [tex]\textcolor{red}{\,e}[/tex] a massa de um paralelepípedo e de uma esfera, respectivamente. Devido ao equilíbrio da balança podemos concluir que:
[tex]\qquad 2\textcolor{blue}{b}+3\textcolor{red}{e}=13\textcolor{red}{e}[/tex]
[tex]\qquad 2\textcolor{blue}{b}=10\textcolor{red}{e}[/tex]
[tex]\qquad \textcolor{blue}{b}=5\textcolor{red}{e}.[/tex]
Logo, são necessárias [tex]\,\fcolorbox{black}{#eee0e5}{$\text{cinco}$} [/tex] esferas para equilibrar um paralelepípedo.
Solução elaborada pelos Moderadores do Blog.
