Problema
(Indicado a partir do 9º ano do E. F.)
Nos quatro primeiros tiros de uma competição, um atirador situado em um ponto [tex]P[/tex] deveria acertar alvos localizados nos vértices de um retângulo [tex]ABDC[/tex].
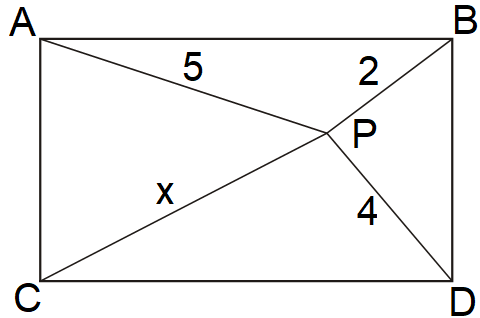
Sabendo que a distância de [tex]A[/tex] a [tex]P[/tex] era de [tex]5[/tex] m, de [tex]B[/tex] a [tex]P[/tex], [tex]2\text{ m}[/tex], de [tex]D[/tex] a [tex]P[/tex], [tex]4\text{ m}[/tex], determine a distância do alvo [tex]C[/tex] a [tex]P[/tex].
Extraído de um simulado do Colégio Ari de Sá.
Solução
Considere a figura a seguir, na qual indicamos diversas medidas obtidas após traçarmos dois segmentos de reta passando pelo ponto [tex]P[/tex] e paralelos aos lados do retângulo.
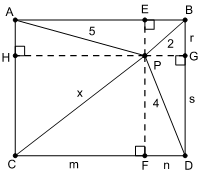
Vamos aplicar o Teorema de Pitágoras em quatro triângulos retângulos:
- Triângulo [tex]APH[/tex]:
- Triângulo [tex]BPE[/tex]:
- Triângulo [tex]DPG[/tex]:
- Triângulo [tex]CPF[/tex]:
[tex]\qquad m^2+r^2=5^2; \qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad n^2+r^2=2^2; \qquad \textcolor{#800000}{(ii)}[/tex]
[tex]\qquad n^2+s^2=4^2; \qquad \textcolor{#800000}{(iii)}[/tex]
[tex]\qquad m^2+s^2=x^2. \qquad \textcolor{#800000}{(iv)}[/tex]
Agora, vamos somar as igualdades [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], assim como [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iv)}[/tex], obtendo respectivamente,
[tex]\qquad m^2+r^2+n^2+s^2=5^2+4^2, \qquad \textcolor{#800000}{(v)}[/tex]
[tex]\qquad n^2+r^2+m^2+s^2=2^2+x^2. \qquad \textcolor{#800000}{(vi)}[/tex]
Comparando [tex]\textcolor{#800000}{(v)}[/tex] e [tex]\textcolor{#800000}{(vi)}[/tex], segue que:
[tex]\qquad 2^2+x^2=5^2+4^2[/tex]
[tex]\qquad 4+x^2=25+16[/tex]
[tex]\qquad x^2=37[/tex]
[tex]\qquad \,\fcolorbox{black}{#eee0e5}{$x=\sqrt{37}\text{ m}$}[/tex],
já que [tex]x \geqslant 0[/tex], pois representa um comprimento.
Solução elaborada pelos Moderadores do Blog.
