Problema
(Indicado a partir do 9º ano do E. F.)
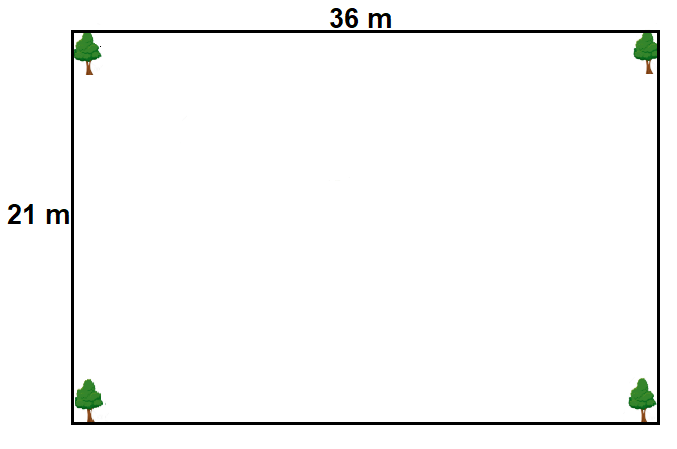
(Números e Operações, Marília Centurion – Adaptado) O dono de um terreno retangular de 36 metros de comprimento por 21 metros de largura deseja cercá-lo com eucaliptos plantados com distâncias iguais um do outro, e quer manter, entre os eucaliptos, a maior distância possível, medida em um número inteiro de metros. Se em cada canto do terreno for plantado um eucalipto, qual será a distância entre eles e quantos eucaliptos serão necessários?
Solução 1
Para resolver este problema deve-se verificar qual é o maior número inteiro positivo que divide em partes iguais tanto [tex]36[/tex] como [tex]21[/tex]. Denotando por [tex]D(n)[/tex] o conjunto dos divisores positivos do número inteiro positivo [tex]n[/tex], os divisores de [tex]36[/tex] são os elementos do conjunto
[tex]\qquad D(36) = \{1, 2, 3, 4, 6, 9, 12, 18, 36 \}[/tex]
e, os divisores de [tex]21[/tex], os elementos de
[tex]\qquad D(21) = \{1, 3, 7, 21 \}.[/tex]
Assim, o maior número que é divisor comum de [tex] 36 [/tex] e [tex] 21[/tex] é o [tex]3 [/tex], ou seja, [tex] mdc(36, 21)=3[/tex]. Observe que esse valor também pode ser obtido utilizando-se o Algoritmo de Euclides, conforme apresentado nesta Sala:
|
[tex]\begin{array}{r} 36\,\,\end{array} \begin{array}{|r} \,21\,\, \\ \hline \end{array}[/tex] [tex]\begin{array}{r} 15 \end{array}\begin{array}{r} \quad 1 \end{array}[/tex] |
[tex]\qquad \qquad \begin{array}{r} 21\,\,\end{array} \begin{array}{|r} \,15\,\, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} \,6 \end{array}\begin{array}{r} \quad \,\, 1 \end{array}[/tex] |
[tex]\qquad \qquad \begin{array}{c} 15\,\,\end{array} \begin{array}{|c} \,6\,\,\, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{c} \, 3\, \end{array}\begin{array}{c} \quad 2 \end{array}[/tex] |
[tex]\qquad \qquad \begin{array}{r} 6\,\,\end{array} \begin{array}{|r} \,3\,\,\, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} 0 \end{array}\begin{array}{r} \,\,\,\, 2 \end{array}[/tex] |
Portanto, [tex]mdc(36, 21) = mdc(21, 15) = mdc(6, 15) = mdc(6, 3) = 3 [/tex].
Como o maior número divisor comum de [tex] 36 [/tex] e [tex] 21[/tex] é igual a [tex] 3 [/tex], então os eucaliptos devem ser plantados a cada [tex]3[/tex] metros. Vejamos quantos eucaliptos serão necessários:
- Nos [tex]4[/tex] cantos do terreno, devemos colocar [tex]4[/tex] árvores: uma em cada canto.
- Sendo de [tex]3\, m[/tex] o espaçamento entre as árvores, haverá [tex]36\div 3=12[/tex] espaços em cada um dos maiores lados. Como nos cantos já estão colocadas árvores, colocamos mais [tex]22[/tex] árvores nos dois maiores lados, sendo [tex]11[/tex] em cada lado.
- Da mesma forma, como o espaçamento entre as árvores é de [tex]3\, m[/tex], haverá [tex]21\div 3=7[/tex] espaços em cada um dos menores lados. Como nos cantos já estão colocadas árvores, colocamos mais [tex]12[/tex] árvores distribuídas nos lados menores, [tex]6[/tex] em cada um.
Totalizamos, então, [tex]\,\fcolorbox{black}{#eee0e5}{$4+22+12=38$}\,[/tex] árvores, conforme ilustra a figura a seguir.

Solução elaborada pelos Moderadores do Blog.
Solução 2
Como o MDC de [tex]36 [/tex] e [tex]21 [/tex] é igual a [tex] 3[/tex] (veja os cálculos na Solução 1), então os eucaliptos devem ser plantados a cada [tex]3[/tex] metros. Vejamos quantos eucaliptos serão necessários.
- Na lateral do terreno que mede [tex]21[/tex] metros, temos [tex]21:3=7[/tex] espaços de [tex]3\text{ m}[/tex], ou seja, um total de [tex]8[/tex] árvores plantadas nessa lateral.
- Na lateral do terreno que mede [tex]36[/tex] metros, temos [tex]36:3=12[/tex] espaços de [tex]3\text{ m}[/tex], ou seja, um total de [tex]13[/tex] árvores plantadas nessa lateral.
- Para finalizar, perceba que as árvores plantadas em cada canto do terreno foram contadas duas vezes, uma vez para cada lateral que forma aquele canto, o que nos leva a diminuir [tex]4[/tex] árvores, referentes aos [tex]4[/tex] cantos. Desta forma, a quantidade correta de árvores plantadas deve ser [tex]\,\fcolorbox{black}{#eee0e5}{$8+8+13+13-4=38$}\,.[/tex]
Observe como fica a plantação:
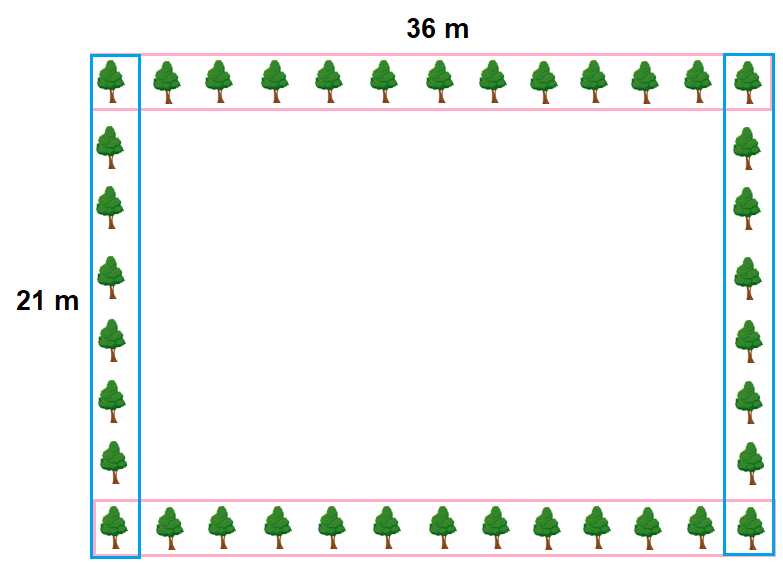
Solução elaborada pelos Moderadores do Blog.
