Problema – Três circunferências e um triângulo
Na figura abaixo, vemos três circunferências coplanares, duas a duas tangentes exteriores, com centros nos pontos A, B e C e com raios medindo [tex]2\text{ cm}[/tex], [tex]4\text{ cm}[/tex] e [tex]5\text{ cm}[/tex] respectivamente.
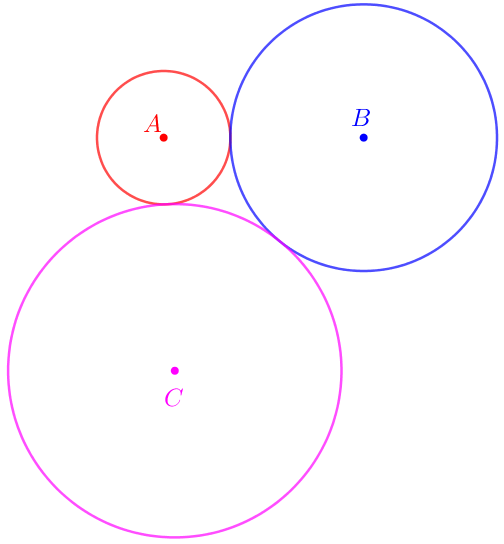
Determinar a área e o perímetro do triângulo ABC.
Um desafio extra: Usando régua e compasso, você saberia construir essas três circunferências a partir das medidas dos três raios?
Você não deve estar acostumado a esse tipo de construção. Mas, acredite, não é difícil fazê-la e é um belo passatempo. Para esquentar os motores, faça primeiro uma construção mais simples:
- Conhecendo a medida dos raios de duas circunferências não tangentes entre si (nem interior nem exteriormente), construa uma terceira que seja tangente exterior às duas iniciais.
Bom divertimento!
 |
Se vocês precisarem de uma ajuda para fazer a construção das três circunferências, a partir das medidas dos três raios, utilizem o applet abaixo.
|
Um applet para ajudar no desafio
Passo 1: Com a régua, construa uma reta auxiliar [tex]r[/tex] e nela marque o ponto [tex]A[/tex].
Passo 2: Com o compasso, transfira a medida do segmento [tex]\overline{P_1Q_1}[/tex] para a reta [tex]r[/tex], a partir de [tex]A[/tex]. Para isso, construa um segmento [tex]\overline{AT_1}[/tex] sobre [tex]r[/tex] que seja congruente ao segmento [tex]\overline{P_1Q_1}[/tex] e, portanto, tenha comprimento [tex]2\text{ cm}[/tex]. Marque o ponto [tex]T_1[/tex] à direita de [tex]A\,.[/tex]
Passo 3: Com o compasso, construa a circunferência [tex]\textcolor{red}{\lambda_1}[/tex] de centro em [tex]A[/tex] e que passa por [tex]T_1.[/tex] Essa será a nossa circunferência de raio [tex]2\text{ cm}[/tex].
Passo 4: Use novamente o compasso e transfira a medida do segmento [tex]\overline{P_2Q_2}[/tex] para a reta [tex]r[/tex]. Para isso, construa um segmento [tex]\overline{T_1B}[/tex] sobre [tex]r[/tex] que seja congruente ao segmento [tex]\overline{P_2Q_2}[/tex] e, portanto, tenha comprimento [tex]4\text{ cm}[/tex]. Marque o ponto [tex]B[/tex] à direita de [tex]T_1\,.[/tex]
Passo 5: Com o compasso, construa a circunferência [tex]\textcolor{blue}{\lambda_2}[/tex] de centro em [tex]B[/tex] e que passa por [tex]T_1.[/tex] Essa será a nossa circunferência de raio [tex]4\text{ cm}[/tex].
Já temos duas circunferências tangentes externas com raios de comprimentos [tex]2\text{ cm}[/tex] e [tex]4\text{ cm}[/tex]. O ponto [tex]T_1[/tex] é o ponto de tangência das duas circunferências.
Vamos construir uma terceira circunferência, [tex]\textcolor{#FF00FF}{\lambda_3}[/tex], que tenha raio de [tex]5\text{ cm}[/tex] e que seja tangente externa às duas circunferências [tex]\textcolor{red}{\lambda_1}[/tex] e [tex]\textcolor{blue}{\lambda_2}.[/tex] A ideia é fazer, inicialmente, o Passo 4 e transportar a medida do segmento [tex]\overline{P_3Q_3}[/tex] a partir de [tex]\textcolor{red}{\lambda_1}[/tex] e de [tex]\textcolor{blue}{\lambda_2}[/tex]. Para isso, vamos construir mais duas retas auxiliares para "somarmos" os raios [tex]2\text{ cm}[/tex] e [tex]5\text{ cm}[/tex], assim como os raios [tex]4\text{ cm}[/tex] e [tex]5\text{ cm}\,.[/tex]
Passo 6: Com a régua, construa uma reta auxiliar [tex]r_1[/tex] que contenha o ponto [tex]A[/tex] e denomine [tex]C_1[/tex] uma das interseções de [tex]r_1[/tex] com [tex]\textcolor{red}{\lambda_1}[/tex].
Passo 7: Com a régua, construa uma reta auxiliar [tex]r_2[/tex] que contenha o ponto [tex]B[/tex] e denomine [tex]C_2[/tex] uma das interseções de [tex]r_2[/tex] com [tex]\textcolor{blue}{\lambda_2}.[/tex]
Passo 8: Use o compasso e transfira a medida do segmento [tex]\overline{P_3Q_3}[/tex] para a reta [tex]r_1[/tex], a partir de [tex]C_1[/tex]. Para isso, construa um segmento [tex]\overline{C_1D_1}[/tex] sobre [tex]r_1[/tex] que seja congruente ao segmento [tex]\overline{P_3Q_3}[/tex] e, portanto, tenha comprimento [tex]5\text{ cm}[/tex]. Pela maneira com que construímos [tex]r_1[/tex] e escolhemos [tex]C_1[/tex], marque o ponto [tex]D_1[/tex] abaixo de [tex]C_1\,.[/tex]
Passo 9: Use o compasso e transfira a medida do segmento [tex]\overline{P_3Q_3}[/tex] para a reta [tex]r_2[/tex], a partir de [tex]C_2[/tex]. Para isso, construa um segmento [tex]\overline{C_2D_2}[/tex] sobre [tex]r_2[/tex] que seja congruente ao segmento [tex]\overline{P_3Q_3}[/tex] e, portanto, tenha comprimento [tex]5\text{ cm}[/tex]. Pela maneira com que construímos [tex]r_2[/tex] e escolhemos [tex]C_2[/tex], marque o ponto [tex]D_2[/tex] abaixo de [tex]C_2\,.[/tex]
Perceba que:
- a circunferência de centro em [tex]A[/tex] e que passa por [tex]D_1[/tex] contém todos os possíveis centros de circunferência com raios [tex]5\text{ cm}[/tex] que são tangentes à circunferência [tex]\textcolor{red}{\lambda_1}[/tex];
- a circunferência de centro em [tex]B[/tex] e que passa por [tex]D_2[/tex] contém todos os possíveis centros de circunferência com raios [tex]5\text{ cm}[/tex] que são tangentes à circunferência [tex]\textcolor{blue}{\lambda_2}[/tex].
Assim, as interseções dessas duas circunferências nos fornecerão pontos que são centros de circunferência com raios [tex]5\text{ cm}[/tex] que são tangentes simultaneamente às circunferências [tex]\textcolor{red}{\lambda_1}[/tex] e [tex]\textcolor{blue}{\lambda_2}.[/tex] Para não sobrecarregar o nosso desenho, ao invés de traçarmos essas duas circunferências, traçaremos apenas arcos delas: [tex]\textcolor{red}{\gamma_1}[/tex] e [tex]\textcolor{blue}{\gamma_2}.[/tex]
Passo 10: Com o compasso, construa o arco de circunferência [tex]\textcolor{red}{\gamma_1}[/tex] de centro em [tex]A[/tex] e que passa por [tex]D_1.[/tex]
Passo 11: Com o compasso, construa o arco de circunferência [tex]\textcolor{blue}{\gamma_2}[/tex] de centro em [tex]B[/tex] e que passa por [tex]D_2.[/tex]
Finalmente temos o centro da nossa terceira circunferência, [tex]\textcolor{#FF00FF}{\lambda_3}[/tex].
Passo 12: Denote por [tex]C[/tex] a interseção dos arcos [tex]\textcolor{red}{\gamma_1}[/tex] e [tex]\textcolor{blue}{\gamma_2}[/tex].
Passo 13: Com o compasso tome a medida do segmento [tex]\overline{P_3Q_3}[/tex] e, com essa medida, trace a circunferência [tex]\textcolor{#FF00FF}{\lambda_3}[/tex] com centro em [tex]C[/tex] e o raio com a medida do segmento [tex]\overline{P_3Q_3}.[/tex]
Passo 14: Observe o ponto de tangência [tex]T_2[/tex] das circunferências [tex]\textcolor{red}{\lambda_1}[/tex] e [tex]\textcolor{#FF00FF}{\lambda_3}[/tex] e o ponto de tangência [tex]T_3[/tex] das circunferências [tex]\textcolor{blue}{\lambda_2}[/tex] e [tex]\textcolor{#FF00FF}{\lambda_3}.[/tex]
Instruções para utilização do applet:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para acompanhar os passos definidos para a construção das circunferências, clique sucessivamente nos quadradinhos que irão aparecer.
(3) Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
 |
Para ver uma solução deste problema, clique aqui .
|
Equipe COM – OBMEP
 |
Se for conveniente, você pode utilizar o applet off-line. Para isso, copie o arquivo abaixo e abra-o no GeoGebra do seu computador ou tablet. |
