Problema – Relação entre áreas em um tetraedro
A figura mostra um tetraedro [tex]ABCD[/tex] cujos vértices [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] são vértices de um paralelepípedo retangular de dimensões com medidas [tex]x[/tex], [tex]y[/tex] e [tex]z[/tex].
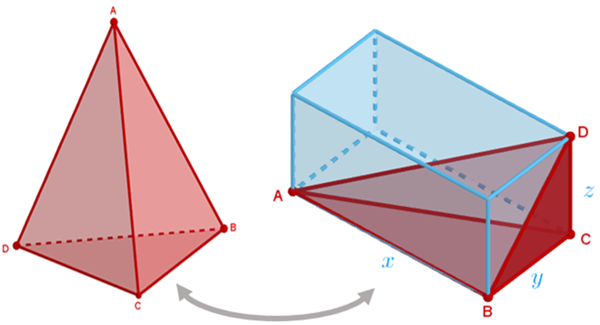
Se [tex]F_A[/tex], [tex]F_B[/tex], [tex]F_C[/tex] e [tex]F_D[/tex] são as áreas das faces do tetraedro opostas, respectivamente, aos vértices [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex], prove que [tex]\boxed{F^2_A + F^2_C= F^2_B + F^2_D}[/tex].
(Extraído de Maclaurin Olympiad, 2003-2009)
 |
Se vocês precisarem de uma ajuda para visualizar melhor o tetraedro e o paralelepípedo, utilizem o applet abaixo.
|
Um applet para ajudar
Instruções:
(1) Espere o applet carregar. (O aplicativo abrirá uma janela 3D; assim, ele pode demorar um pouquinho para carregar.)
(2) Para movimentar o paralelepípedo e, consequentemente, o tetraedro, clique em qualquer lugar da janela do aplicativo, mantenha o mouse pressionado e faça o movimento.
(3) Se quiser voltar para a posição inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
 |
Para ver uma solução deste problema, clique aqui .
|
Equipe COM – OBMEP
 |
Se for conveniente, você pode utilizar o applet off-line. Para isso, copie o arquivo abaixo e abra-o no GeoGebra do seu computador ou tablet. |
