Problema
(Indicado a partir do 2º ano do E. M.)
Seja [tex]ABCDEF[/tex] um hexágono regular inscrito numa circunferência de centro [tex]O[/tex] e raio [tex]6[/tex] cm.
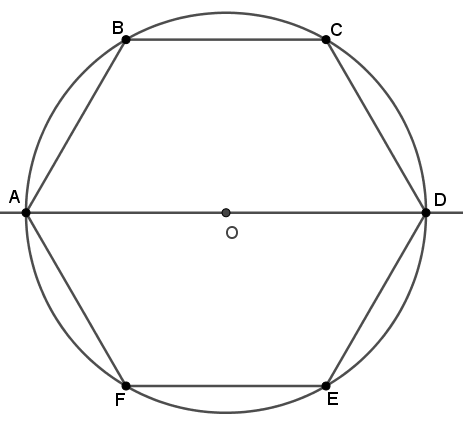
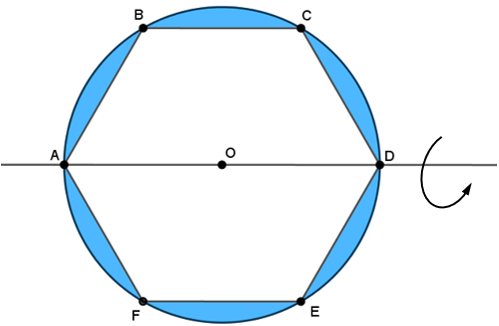
Considere a região interior à circunferência e exterior ao hexágono. Determine o volume do sólido gerado pela rotação completa dessa região em torno do eixo que passa pelos pontos [tex]A[/tex] e [tex]D[/tex].
Lembretes:
I) Volume do cilindro de revolução de raio da base [tex]r[/tex] e altura [tex]h[/tex]: [tex]\boxed{V_{Cilindro}=\pi \cdot r^{2}\cdot h}\,.[/tex]
II) Volume do cone de revolução de raio da base [tex]r[/tex] e altura [tex]h[/tex]: [tex]\boxed{V_{Cone}=\dfrac{1}{3}\cdot\pi \cdot r^{2}\cdot h}\,.[/tex]
III) Volume da esfera de raio [tex]r[/tex]: [tex]\boxed{V_{Esfera}=\dfrac{4}{3}\pi \cdot r^{3}}\,.[/tex]
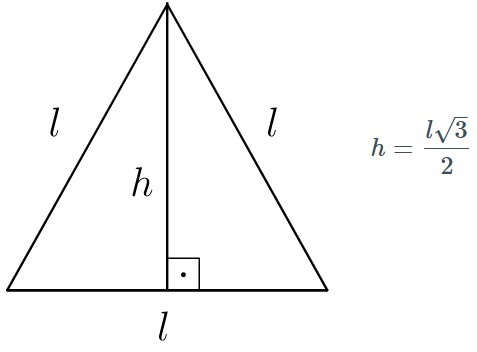
IV) Um triângulo equilátero de lado medindo [tex]l[/tex] tem altura dada por [tex]h = \dfrac{l\sqrt{3}}{2}\,.[/tex]
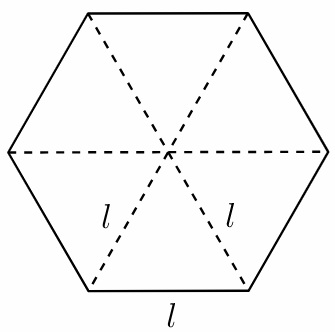
V) Dado um hexágono regular de lado medindo [tex]l[/tex] este pode ser dividido em [tex]6[/tex] triângulos equiláteros de lado medindo [tex]l[/tex].
Solução
Observe que a rotação do hexágono produz dois cones (de vértices [tex]A[/tex] e [tex]D[/tex]) e um cilindro central.
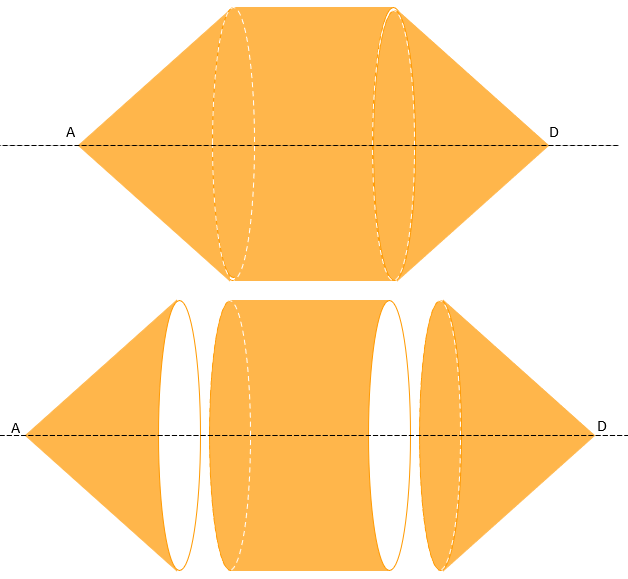
Assim, o volume do sólido gerado pela rotação da região colorida de azul em torno do eixo que passa pelos pontos [tex]A[/tex] e [tex]D[/tex] é o volume de uma esfera de raio [tex]6[/tex] cm menos o volume dos três sólidos mostrados acima. As medidas necessárias para os cálculos são mostradas na figura a seguir. Utilizamos as informações dos lembretes IV e V para obtê-las, além de lembrarmos que a altura de um triângulo equilátero é também sua mediana.
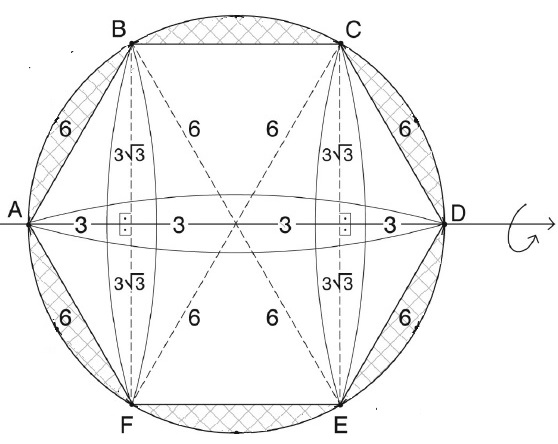
Vamos aos cálculos:
[tex]\qquad V_{sólido\;gerado}=V_{Esfera}-V_{Cilindro}-2 \cdot V_{Cone}\\
\qquad V_{sólido\;gerado}=\dfrac{4}{3}\cdot\pi\cdot 6^{3}- \pi \cdot(3\sqrt{3})^{2}\cdot6 – 2\cdot\dfrac{1}{3}\cdot\pi\cdot(3\sqrt{3})^{2}\cdot 3\\
\qquad V_{sólido\;gerado}=288 \pi -162 \pi -54 \pi\\
\qquad \fcolorbox{black}{#eee0e5}{$V_{sólido\;gerado}=72\pi \text{ cm}^{3}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.