Problema
(Indicado a partir do 2º ano do E. M.)
Quantos polígonos convexos podemos formar utilizando apenas vértices, não necessariamente todos, do eneágono mostrado abaixo?
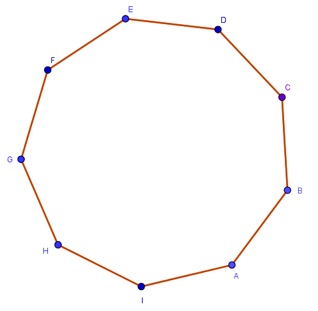

Ajuda
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{ , com } n,r\in\mathbb{N} \text{ e } r\leqslant n[/tex].
Na solução deste problema será utilizada a seguinte propriedade das Combinações simples:
[tex]\qquad \qquad \boxed{ C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+ \cdots\ +C_{n}^{n}=2^{n}}\,.[/tex]
Solução
Inicialmente, vamos calcular quantos triângulos (polígonos de três vértices) podemos formar a partir dos nove vértices do eneágono. De acordo com a Ajuda, isso pode ser feito de [tex]C_{9}^{3}[/tex] maneiras. Agora, vamos calcular o número de quadriláteros (polígonos de quatro vértices): isso pode ser feito de [tex]C_{9}^{4}[/tex] maneiras.
Podemos usar esse mesmo raciocínio para polígonos de cinco, seis, sete, oito e nove vértices e, portanto, de acordo com a Ajuda, teremos:
► [tex]C_{9}^{3}[/tex] polígonos com três vértices;
► [tex]C_{9}^{4}[/tex] polígonos com quatro vértices;
► [tex]C_{9}^{5}[/tex] polígonos com cinco vértices;
► [tex]C_{9}^{6}[/tex] polígonos com seis vértices;
► [tex]C_{9}^{7}[/tex] polígonos com sete vértices;
► [tex]C_{9}^{8}[/tex] polígonos com oito vértices e
► [tex]C_{9}^{9}[/tex] polígonos com nove vértices.
(Observe que nessas contagens que fizemos levamos em consideração que, "dado um conjunto de vértices, há um e somente um polígono convexo com exatamente aqueles vértices".)
Somando essas sete quantidades, obtemos que o total [tex]T[/tex] de polígonos possíveis de serem construídos é:
[tex]\quad T=C_{9}^{3}+C_{9}^{4}+C_{9}^{5}+C_{9}^{6}+C_{9}^{7}+C_{9}^{8}+C_{9}^{9}[/tex].
Mas, qual o valor final de [tex]T[/tex]?
Pela propriedade apresentada na Ajuda sabemos que:
[tex]\qquad C_{9}^{0}+C_{9}^{1}+C_{9}^{2}+C_{9}^{3}+C_{9}^{4}+C_{9}^{5}+C_{9}^{6}+C_{9}^{7}+C_{9}^{8}+C_{9}^{9}=2^{9}[/tex];
portanto, segue que:
[tex]\qquad T=C_{9}^{3}+C_{9}^{4}+C_{9}^{5}+C_{9}^{6}+C_{9}^{7}+C_{9}^{8}+C_{9}^{9}\\
\qquad T= C_{9}^{0}+C_{9}^{1}+C_{9}^{2}+ \cdots\ +C_{9}^{9}-\left(C_{9}^{0}+C_{9}^{1}+C_{9}^{2}\right)\\
\qquad T=2^{9}-\left(C_{9}^{0}+C_{9}^{1}+C_{9}^{2}\right)\\
\qquad T=512-\left(1+9+36\right)\\
\qquad T=512-46=466\,.[/tex]
Logo, podemos construir [tex] \fcolorbox{black}{#eee0e5}{$466$}\,[/tex] polígonos convexos, utilizando apenas vértices do eneágono.
Solução elaborada pelos Moderadores do Blog.
