Problema
(Indicado a partir do 9º ano do E. F.)
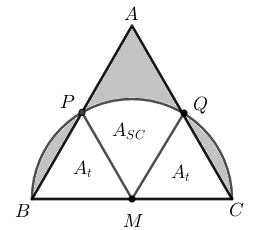
Calcule a área sombreada que aparece na figura abaixo, sabendo que [tex]ABC[/tex] é um triângulo equilátero e que sobre [tex]\overline{BC}[/tex] foi construído um semicírculo de raio [tex]1\text{ cm}[/tex].
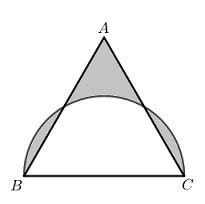
Adaptado da II Olimpíada do Mercosul, 1997.

Lembretes e Notações
[tex]\textcolor{#800000}{(i)}[/tex] Todo triângulo isósceles com um ângulo medindo [tex]60^{\circ}[/tex] é equilátero.
[tex]\textcolor{#800000}{(ii)}[/tex] A área [tex]A[/tex] de um triângulo equilátero de lado [tex]l[/tex] é [tex]A=\dfrac{l^2\sqrt{3}}{4}[/tex]
[tex]\textcolor{#800000}{(iii)}[/tex] A área [tex]A[/tex] de um semicírculo de raio [tex]r[/tex] é [tex]A=\dfrac{\pi\cdot r^2}{2}[/tex].
[tex]\textcolor{#800000}{(iv)}[/tex] A área [tex]A[/tex] de um setor circular de raio [tex]r[/tex] e ângulo [tex]\alpha[/tex], em graus, é [tex]A=\dfrac{\pi\cdot r^2\cdot \alpha}{360}[/tex].
Notações:
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex] Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
– Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\angle XVY. [/tex]
Solução
Inicialmente, notemos que o lado [tex]\overline{BC}[/tex] do triângulo equilátero que aparece na figura do problema é o diâmetro do semicírculo e este possui raio igual a [tex]1\text{ cm}[/tex]. Então, [tex]AB=BC=AC=2\text{ cm}[/tex].
Para a solução do problema, consideraremos o ponto médio [tex]M[/tex] do lado [tex]\overline{BC}[/tex] e os pontos [tex]P[/tex] e [tex]Q[/tex], interseções entre o semicírculo da figura e os lados [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] do triângulo equilátero, respectivamente.
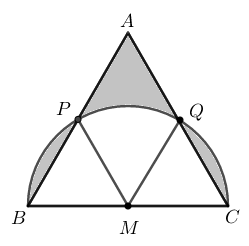
Vemos que [tex]MB=MP=MQ=MC=1\text{ cm}\,[/tex], pois são raios do semicírculo; assim, os triângulos [tex]BMP, \;PMQ[/tex] e [tex]QMC[/tex] são isósceles e, como o triângulo [tex]ABC[/tex] é equilátero, então [tex]\angle PBM=\angle QCM=60^{\circ}[/tex].
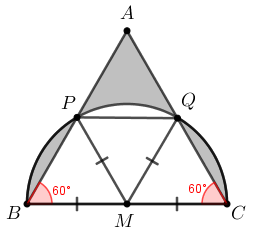
Pelo [tex]\textcolor{#800000}{\textbf{Lembrete (i)}}[/tex], os triângulos [tex]BMP[/tex] e [tex]QMC[/tex] são equiláteros; consequentemente, temos que [tex]\angle PMB=\angle QMC=60^{\circ}[/tex] e [tex]\angle PMQ=180^\circ-2\cdot 60^\circ=60^{\circ}[/tex], o que implica que o setor circular [tex]MPQ[/tex] tem raio [tex]1\text{ cm}[/tex] e um ângulo de [tex]60^\circ\,.[/tex]
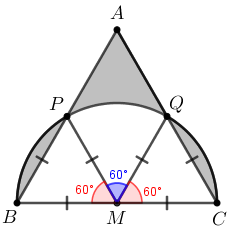
Agora, para efeito dos nossos cálculos, vamos considerar:
- [tex]A_S:[/tex] área da parte sombreada;
- [tex]A_{SM}:[/tex] área do semicírculo;
- [tex]A_T:[/tex] área do triângulo equilátero [tex]ABC[/tex] de lado [tex]2\text{ cm}[/tex];
- [tex]A_t:[/tex] área dos triângulos equiláteros de lado [tex]1\text{ cm}[/tex];
- [tex]A_{SC}:[/tex] área do setor circular.
Dessa forma, a área sombreada, [tex]A_S[/tex], é dada por
[tex]\qquad A_S=(A_T-2A_t-A_{SC})\textcolor{red}{+}(A_{SM}-2A_t-A_{SC})[/tex]
[tex]\qquad A_S=A_T+A_{SM}-4A_t-2A_{SC}.[/tex]
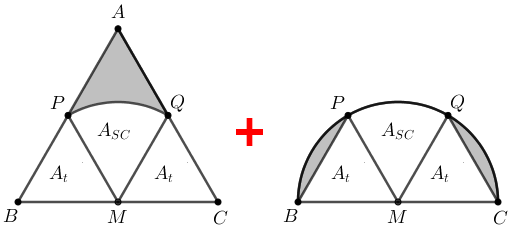
Utilizando os [tex]\textcolor{#800000}{\textbf{Lembretes (ii)}}[/tex], [tex]\textcolor{#800000}{\textbf{(iii)}}[/tex] e [tex]\textcolor{#800000}{\textbf{(iv)}}[/tex] temos:
[tex]\qquad A_S=\dfrac{2^2\cdot \sqrt{3}}{4}+\dfrac{\pi\cdot 1^2}{2}-4\cdot \dfrac{1^2\cdot \sqrt{3}}{4}-2\cdot \dfrac{\pi\cdot 1^2\cdot 60}{360}\\
\qquad A_S=\sqrt{3}+\dfrac{\pi}{2}-4\cdot \dfrac{\sqrt{3}}{4}-2\cdot \dfrac{\pi}{6}\\
\qquad A_S=\sqrt{3}+\dfrac{\pi}{2}-\sqrt{3}-\dfrac{\pi}{3}\\
\qquad A_S=\dfrac{\pi}{2}-\dfrac{\pi}{3}\\
\qquad A_S=\dfrac{3\pi-2\pi}{6}\\
\qquad \fcolorbox{black}{#eee0e5}{$A_S=\dfrac{\pi}{6}\text{ cm}^2$}\,.[/tex]
Por curiosidade, observe que [tex]A_S=A_{SC}[/tex].
Solução elaborada pelos Moderadores do Blog.
