Problema
(Indicado a partir do 9º ano do E. F.)
A figura abaixo mostra duas semicircunferências de diâmetros [tex]AB = 4\text{ cm}[/tex] e [tex]AC = 6\text{ cm}[/tex]. Calcule o raio da circunferência que é tangente às duas semicircunferências e ao segmento [tex]\overline{BC}[/tex].
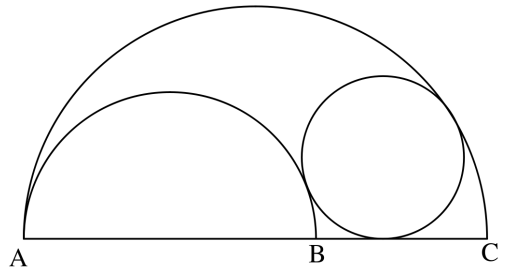
(Extraído de Teorema de Pitágoras e Áreas, Apostila do PIC-OBMEP)
Lembretes
[tex] \textcolor{#800000}{(1)}[/tex] Em um triângulo de lados medindo [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], a fórmula de Herão nos garante que a área [tex]A[/tex] desse triângulo é:
[tex]A=\sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}[/tex], onde [tex]p=\dfrac{a+b+c}{2}\,.[/tex]
(Se você não se lembra da fórmula de Herão, seria interessante dar uma passadinha nesta Sala de Estudo.)
[tex] \textcolor{#800000}{(2)}[/tex] Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB[/tex].
Solução
Sejam [tex]M[/tex] e [tex]N[/tex] os centros das semicircunferências de diâmetros [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex], respectivamente, [tex]P[/tex] o centro da circunferência e [tex]R[/tex] o ponto de tangência entre a circunferência e a semicircunferência de diâmetro [tex]\overline{AB}[/tex].
Sendo [tex]PR=PS=PT=x[/tex], então [tex]MA=MR=2[/tex], [tex]MN=1[/tex] e [tex]NP=3-x[/tex].
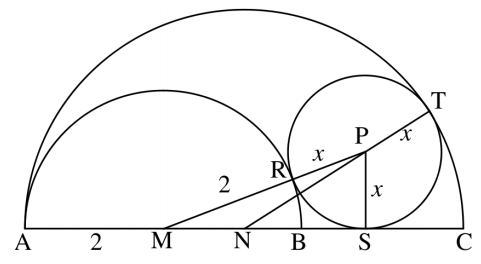
Veja que o semiperímetro [tex]p[/tex] do triângulo [tex]MNP[/tex] é:
[tex]\qquad p=\dfrac{2+x+3-x+1}{2}=3[/tex];
assim, utilizando o Lembrete 1, a área deste mesmo triângulo é dada por
[tex]\qquad S_{MNP}=\sqrt{3\cdot(3-(2+x))\cdot(3-(3-x))\cdot(3-1)}\\
\qquad \boxed{S_{MNP}=\sqrt{3\cdot(3-2-x)\cdot(3-3+x)\cdot(3-1)}}\,.[/tex]
Mas também podemos calcular a área do triângulo [tex]MNP[/tex] pela fórmula [tex]\,\dfrac{\text{base} \times \text{altura}}{2}[/tex]; assim:
[tex]\qquad \boxed{S_{MNP}=\dfrac{1\cdot x}{2}}[/tex],
onde, tomando o segmento [tex]\overline{MN}[/tex] como a base, [tex]\overline{PS}[/tex] é a altura relativa a essa base.
Independentemente de como calculamos as duas áreas, o valor é o mesmo; portanto, segue que:
[tex]\qquad \sqrt{3\cdot(3-2-x)\cdot(3-3+x)\cdot(3-1)}=\dfrac{1\cdot x}{2}\\
\qquad \sqrt{3\cdot(1-x)\cdot x\cdot 2}=\dfrac{x}{2}\\
\qquad 3\cdot(1-x)\cdot x \cdot 2 = \dfrac{x^{2}}{4} \\
\qquad 24x\cdot(1-x) = x^{2} \\
\qquad 25x^{2}-24x=0\\
\qquad x\cdot(25x-24)=0\\
\qquad x=0 \;\text{ ou }\; x=\dfrac{24}{25}=0,96\,.[/tex]
Como [tex]x[/tex] representa um comprimento de raio, então [tex]x\gt0 [/tex] e, portanto, o comprimento do raio da circunferência em questão é [tex] \fcolorbox{black}{#eee0e5}{$0,96 \text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.