Problema
(Indicado a partir do 9º ano do E. F.)
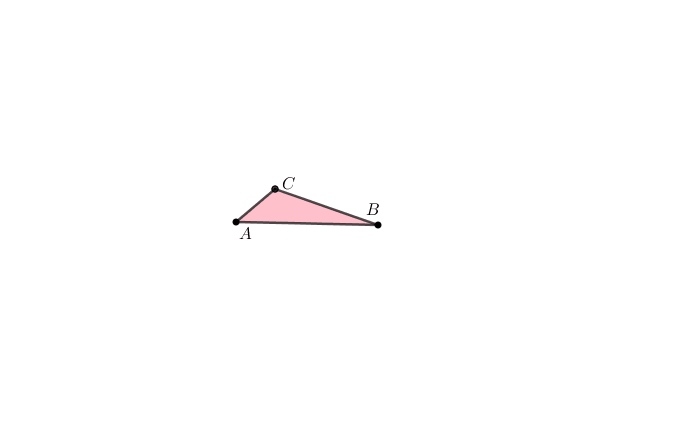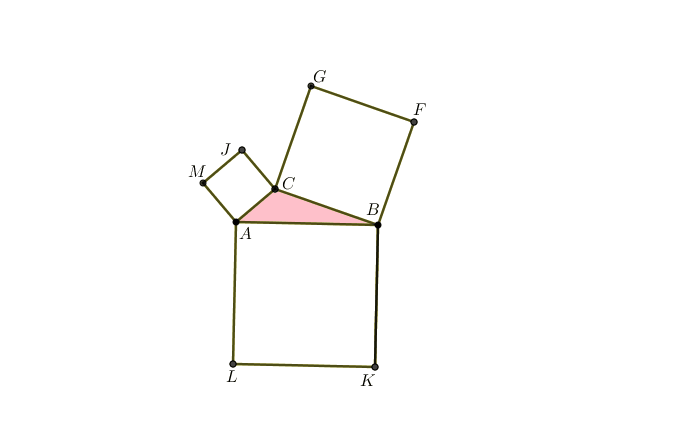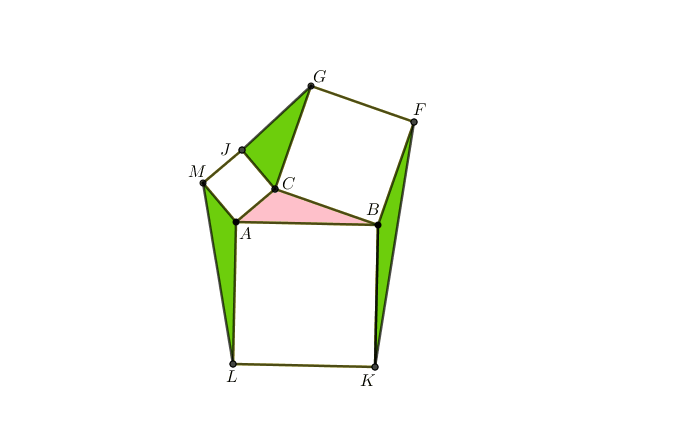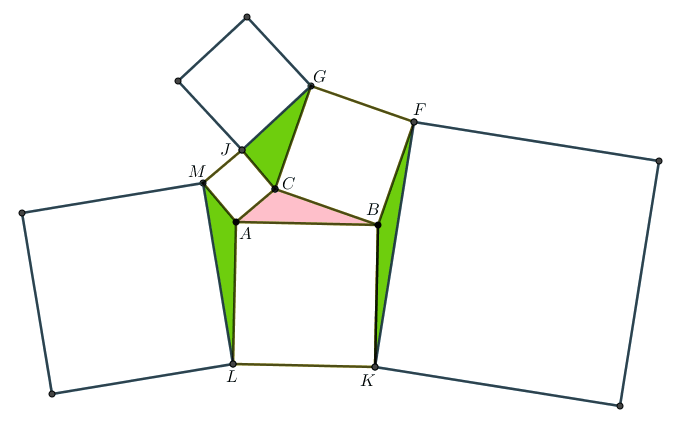
Sobre cada um dos lados de um triângulo [tex]ABC[/tex], foram desenhados os quadrados [tex]ABKL[/tex], [tex]CAMJ[/tex] e [tex]BCGF[/tex], de modo que os lados de cada quadrado tenham exatamente o comprimento do lado do triângulo sobre o qual foi desenhado. Em seguida, foram coloridos de verde os triângulos [tex]ALM[/tex], [tex]CJG[/tex] e [tex]BFK[/tex] e, por fim, foram desenhados mais três quadrados com lados [tex]\overline{LM}[/tex], [tex]\overline{GJ}[/tex] e [tex]\overline{FK}[/tex], respectivamente. A área total dos três quadrados inicialmente desenhados é [tex]A_1[/tex] e a área total dos três últimos quadrados desenhados é [tex]A_2[/tex].
Determine a relação entre [tex]A_1[/tex] e [tex]A_2[/tex].
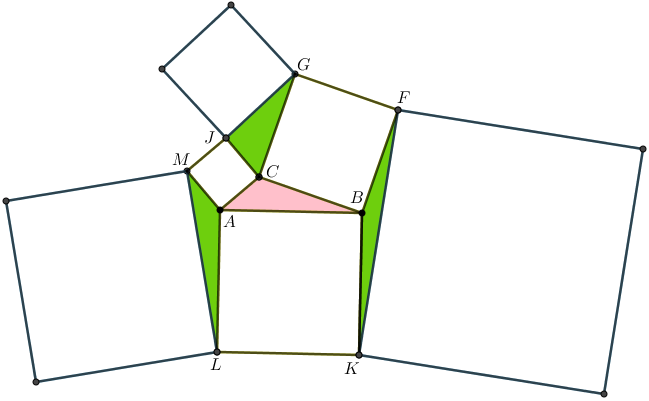
Extraído de Senior Mathematical Challenge,1998 – 2004
AJUDA
Se você ficou com dúvidas com relação à construção da figura, clique no botão abaixo e veja um gif animado.
Solução
Considere [tex]AB=c[/tex], [tex]AC=b[/tex] e [tex]CB=a[/tex] as medidas dos lados do triângulo [tex]ABC[/tex].
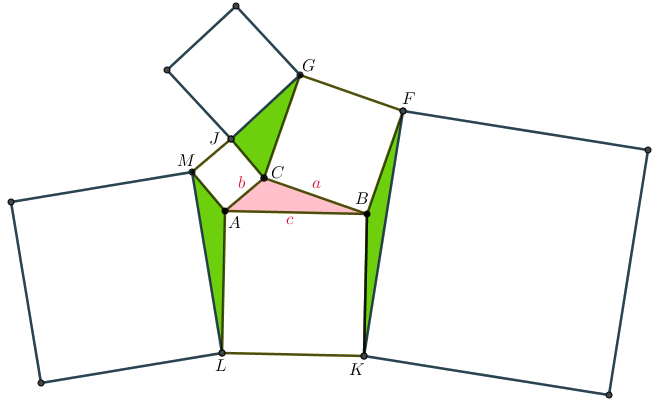
Então, os lados dos três quadrados internos são [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] ; dessa forma, a área total [tex]A_1[/tex] dos três quadrados inicialmente desenhados é [tex]\,\boxed{A_1=a^2+b^2+c^2}\,.[/tex]
Para simplificar notações, denotaremos por [tex]cos\hat{A}[/tex], [tex]cos\hat{B}[/tex] e [tex]cos\hat{C}[/tex] os cossenos relativos às medidas em graus dos ângulos internos [tex]\angle{BAC}[/tex], [tex]\angle{CBA}[/tex] e [tex]\angle{ACB}[/tex] do triângulo [tex]ABC\,[/tex] e vamos identificar os ângulos com suas respectivas medidas.
Agora, vamos aplicar a Lei dos Cossenos no triângulo [tex]ABC[/tex], em relação aos três lados:
[tex]\qquad a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos\hat{A} [/tex],
[tex]\qquad b^2=a^2+c^2-2 \cdot a \cdot c \cdot cos\hat{B} [/tex],
[tex]\qquad c^2=a^2+b^2-2 \cdot a \cdot b \cdot cos\hat{C} [/tex],
e concluir, respectivamente, que:
[tex]\qquad 2 \cdot b \cdot c \cdot cos\hat{A}=b^2+c^2-a^2[/tex], [tex]\qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad 2 \cdot a \cdot c \cdot cos\hat{B}=a^2+c^2-b^2[/tex], [tex] \qquad \textcolor{#800000}{(ii)}[/tex]
[tex]\qquad 2 \cdot a \cdot b \cdot cos\hat{C}=a^2+b^2-c^2[/tex]. [tex] \qquad \textcolor{#800000}{(iii)}[/tex]
- Perceba que no triângulo [tex]MAL[/tex] temos, diretamente, as seguintes medidas: [tex]MA=b[/tex], [tex]LA=c[/tex], e podemos calcular a medida [tex]\angle{MAL}[/tex], em graus, do ângulo [tex]\angle{MAL}[/tex]:
[tex]\qquad \angle{MAL}=360^\circ-90^\circ-90^\circ–\hat{A}=180^\circ-\hat{A}.[/tex]
Aplicando a Lei dos Cossenos no triângulo [tex]MAL[/tex], e observando que [tex]cos(180^\circ-\hat{A})=-cos\hat{A}[/tex], segue que:
[tex]\qquad {ML}^2=b^2+c^2-2 \cdot b \cdot c \cdot cos(180^\circ-\hat{A})[/tex]
[tex]\qquad {ML}^2=b^2+c^2+2 \cdot b \cdot c \cdot cos\hat{A}[/tex].
Assim, a partir de [tex]\textcolor{#800000}{(i)}[/tex], podemos escrever:
[tex]\qquad {ML}^2=b^2+c^2+ b^2+c^2-a^2[/tex]
[tex]\qquad {ML}^2=2(b^2+c^2)-a^2. \qquad \textcolor{#800000}{(iv)}[/tex] - Fazendo o mesmo procedimento para o triângulo [tex]FBK[/tex], temos as seguintes medidas: [tex]FB=a[/tex], [tex]KB=c[/tex] e podemos calcular a medida [tex]\angle{FBK}[/tex], em graus, do ângulo [tex]\angle{FBK}[/tex]:
[tex]\qquad \angle{FBK}=360^\circ-90^\circ-90^\circ–\hat{B}=180^\circ-\hat{B}[/tex].
Como [tex]cos(180^\circ -\hat{B})=-cos\hat{B}[/tex], aplicando agora a Lei dos Cossenos no triângulo [tex]FBK[/tex], segue que:
[tex]\qquad {FK}^2=a^2+c^2-2 \cdot a \cdot c \cdot cos(180^\circ-\hat{B})[/tex]
[tex]\qquad {FK}^2=a^2+c^2+2 \cdot a \cdot c \cdot cos\hat{B}[/tex],
donde de [tex]\textcolor{#800000}{(ii)}[/tex], podemos escrever:
[tex]\qquad {FK}^2=a^2+c^2+a^2+c^2-b^2[/tex]
[tex]\qquad {FK}^2=2(a^2+c^2)-b^2. \qquad \textcolor{#800000}{(v)}[/tex] - Fazendo o mesmo procedimento para o triângulo [tex]GCJ[/tex], temos as seguintes medidas: [tex]GC=a[/tex], [tex]JC=b[/tex] e o seguinte cálculo para a medida [tex]\angle{GCJ}[/tex], em graus, do ângulo [tex]\angle{GCJ}[/tex]:
[tex]\qquad \angle{GCJ}=360^\circ – 90^\circ – 90^\circ-\hat{C}=180^\circ-\hat{C}[/tex],
valendo ainda [tex]cos(180^\circ -\hat{C})=-cos\hat{C}[/tex].
Apliquemos, agora, a Lei dos Cossenos no triângulo [tex]GCJ[/tex]:
[tex]\qquad {GJ}^2=a^2+b^2-2 \cdot a \cdot b \cdot cos(180^\circ-\hat{C})[/tex]
[tex]\qquad {GJ }^2=a^2+b^2+2 \cdot a \cdot b \cdot cos\hat{C}[/tex],
donde de [tex]\textcolor{#800000}{(iii)}[/tex], podemos escrever:
[tex]\qquad {GJ}^2=a^2+b^2+a^2+b^2-c^2[/tex]
[tex]\qquad {GJ}^2=2(a^2+b^2)-c^2. \qquad \textcolor{#800000}{(vi)}[/tex]
Finalmente, vamos calcular a soma [tex]A_2[/tex] das áreas dos três quadrados externos adicionando as expressões obtidas em [tex]\textcolor{#800000}{(iv)}, \textcolor{#800000}{(v)}[/tex] e [tex]\textcolor{#800000}{(vi)}[/tex]. Veja:
[tex]\qquad A_2={ML}^2+{FK}^2+{GJ}^2[/tex]
[tex]\qquad A_2=\left[2(b^2+c^2)-a^2\right]+\left[2(a^2+c^2)-b^2\right]+\left[2(a^2+b^2)-c^2\right][/tex]
[tex]\qquad A_2=2b^2+2c^2-a^2+2a^2+2c^2-b^2+2a^2+2b^2-c^2[/tex]
[tex]\qquad A_2=3a^2+3b^2+3c^2[/tex]
[tex]\qquad A_2=3(a^2+b^2+c^2)[/tex].
Lembrando que a área total dos três quadrados inicialmente desenhados é [tex]A_1=a^2+b^2+c^2[/tex], concluímos que a relação entre [tex]A_1[/tex] e [tex]A_2[/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$A_2=3A_1$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.