Problema
(Indicado a partir do 9º ano do E. F.)
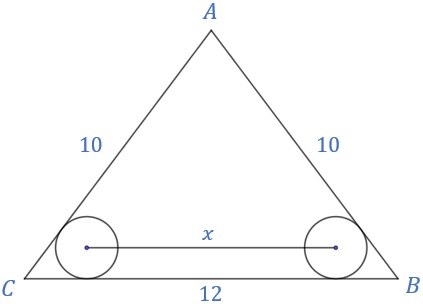
(PAPMEM – IMPA) A figura mostra um triângulo isósceles de lados medindo [tex]10[/tex], [tex]10[/tex] e [tex]12[/tex] centímetros e duas circunferências de raio [tex]1\,\text{cm}[/tex] tangentes a dois lados do triângulo. Calcule a medida [tex]x[/tex] da distância entre os centros das circunferências.
Solução
Inicialmente, vamos construir segmentos dos centros das circunferências aos vértices do triângulo.
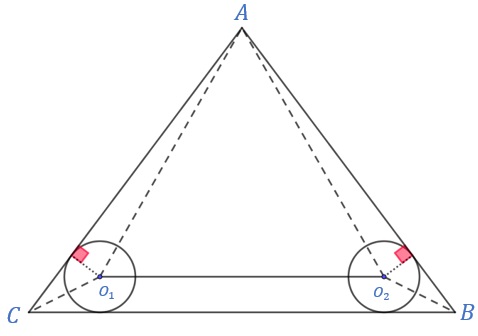
Note que a figura ficou dividida em um trapézio [tex](CO_{1}O_{2}B)[/tex] e três triângulos [tex](AO_{1}O_{2}[/tex], [tex]AO_{1}C[/tex] e [tex]AO_{2}B)[/tex].
Pelo teorema de Pitágoras, podemos encontrar a altura [tex]h[/tex] do triângulo isósceles [tex]ABC[/tex].
[tex]\qquad 10^{2}=h^{2}+6^{2}[/tex]
[tex]\qquad h=8\,\text{cm}.[/tex]
Assim, denotando por [tex]S_{ABC}[/tex] a área do triângulo [tex]ABC[/tex], temos:
[tex]\qquad S_{ABC}=\dfrac{12\cdot 8}{2}=48\,\text{cm}^2.[/tex]
Observe que essa mesma área pode ser calculada somando-se as áreas dos triângulos [tex]AO_{1}O_{2}[/tex], [tex]\,AO_{1}C\,[/tex] e [tex]\,AO_{2}B[/tex] (as quais serão representadas por [tex]S_{AO_{1}O_{2}}[/tex], [tex]\,S_{AO_{1}C}\,[/tex] e [tex]\,S_{AO_{2}B}[/tex], respectivamente) com a área do trapézio [tex]CO_{1}O_{2}B[/tex] (que será representada por [tex]S_{CO_{1}O_{2}B}[/tex]).
Perceba que a altura do trapézio é [tex]1\,\text{cm}[/tex] (raio da circunferência) e, portanto, a altura do triângulo [tex]AO_{1}O_{2}[/tex] é [tex]8-1=7\,\text{cm}[/tex].
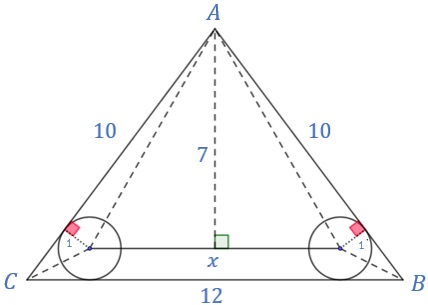
Dessa forma, segue que:
[tex]\qquad S_{CO_{1}O_{2}B}+S_{AO_{1}O_{2}}+S_{AO_{1}C}+S_{AO_{2}B}=48\\
\qquad \dfrac{(12+x)\cdot1}{2}+\dfrac{x\cdot7}{2}+\dfrac{10\cdot1}{2}+\dfrac{10\cdot1}{2}=48\\
\qquad 6+4x+5+5=48\\
\qquad \, \fcolorbox{black}{#eee0e5}{$x=8\,\text{cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
