Problema
(Indicado a partir do 1º ano do E. M.)
(FVG – SP, 2009) Uma editora decidiu disponibilizar o lançamento de um novo livro em duas versões: uma mais elaborada, com capa dura, e outra popular, com capa de papelão. Uma pesquisa realizada pela editora registrou que, no dia do lançamento, o lucro da editora poderia ser estimado pela função:
[tex]L=(25-0,5x)\cdot x+(30-y)\cdot y -(50-0,5x-y)^2[/tex],
na qual [tex]x[/tex] é o preço do exemplar com capa dura e [tex]y[/tex] o preço do exemplar com capa de papelão, em reais.
O departamento de produção da editora decidiu que o exemplar de capa dura deveria custar o dobro do preço do exemplar de capa de papelão. Buscando obter o maior lucro possível, o diretor de vendas estabeleceu estes preços para cada uma das duas versões.
- Capa Dura: [tex]R$\;50,00[/tex].
- Capa de Papelão: [tex]R$\;25,00[/tex].
Foi correta a decisão do diretor de vendas? Justifique.
Solução 1
Pela decisão do departamento de produção da editora, devemos ter [tex]x=2y[/tex] e, portanto, [tex]y=\frac{x}{2}=0,5x[/tex].
Assim, a função que expressa o lucro pode ser reescrita como:
[tex]\qquad L=(25-y)\cdot 2y+(30-y)\cdot y -(50-y-y)^2[/tex]
[tex]\qquad L=50y-2y^{2}+30y-y^{2}-(50-2y)^{2}[/tex]
[tex]\qquad L=80y-3y^{2}-(2500-200y+4y^{2})[/tex]
[tex]\qquad L=80y-3y^{2}-2500+200y-4y^{2}[/tex]
[tex]\qquad L=-7y^{2}+280y-2500[/tex]
Vamos reescrever essa última expressão da seguinte forma:
[tex]\qquad L=-7\cdot (y^{2}-40y)-2500[/tex]
[tex]\qquad L=-7\cdot(y^{2}-40y \textcolor{#FF0000}{+20^{2}-20^{2}}) -2500[/tex]
[tex]\qquad L=-7\cdot(y-20)^2+2800-2500[/tex]
[tex]\qquad L=-7\cdot(y-20)^2+300[/tex]
A última igualdade nos mostra que [tex]L[/tex] não possui valor mínimo, pois o termo do segundo grau está sendo multiplicado por um real negativo. Assim, [tex]L[/tex] só possui valor máximo e esse valor ocorre quando a expressão do segundo grau [tex](y-20)^2[/tex] se anula. Dessa forma, para obtermos o [tex]L[/tex] máximo devemos ter [tex]y-20=0[/tex], ou seja, [tex]y=20.[/tex]
Daí, de [tex]x=2y[/tex], segue que [tex]x=2\cdot 20=\boxed{40}.[/tex]
Portanto, a decisão não foi a correta. A opção que propiciaria lucro máximo seria:
- Capa Dura: [tex] \fcolorbox{black}{#eee0e5}{$ R\$\;40,00$}\,[/tex],
- Capa de Papelão: [tex] \fcolorbox{black}{#eee0e5}{$R\$\;20,00$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.

Ajuda para a Solução 2
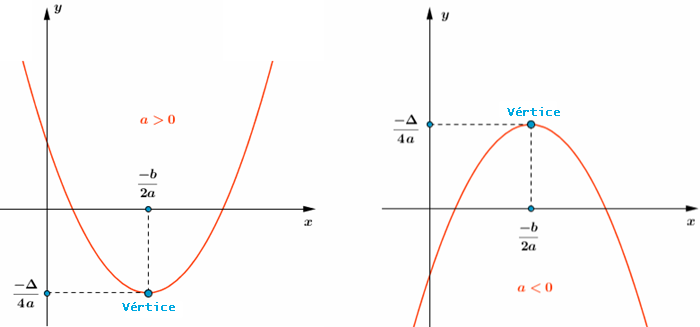
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução 2
Pelo enunciado do problema, devemos ter [tex]x=2y[/tex]; então, a função que expressa o lucro pode ser assim reescrita:
[tex]\qquad L=(25-y)\cdot 2y+(30-y)\cdot y -(50-y-y)^2\\
\qquad L=50y-2y^{2}+30y-y^{2}-(50-2y)^{2}\\
\qquad L=80y-3y^{2}-(2500-200y+4y^{2})\\
\qquad L=80y-3y^{2}-2500+200y-4y^{2}\\
\qquad L=-7y^{2}+280y-2500.[/tex]
Note que a última equação define uma função quadrática em [tex]y[/tex]. Portanto, pela Ajuda, [tex]L[/tex] terá valor máximo quando [tex]y=\dfrac{-280}{2\cdot(-7)}=20[/tex].
Se [tex]y=20 [/tex], então [tex]x=2\cdot20=40[/tex].
Portanto, a decisão não foi a correta. A opção que propiciaria lucro máximo seria:
- Capa Dura: [tex] \fcolorbox{black}{#eee0e5}{$ R\$\;40,00$}\,[/tex],
- Capa de Papelão: [tex] \fcolorbox{black}{#eee0e5}{$R\$\;20,00$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.