Problema
(Indicado a partir do 9º ano do E. F.)
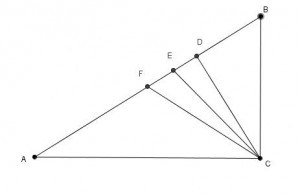
Sendo [tex]ABC[/tex] um triângulo retângulo em [tex]C[/tex], [tex]\overline{CF}[/tex] uma mediana, [tex]\overline{CE}[/tex] uma bissetriz interna e [tex]\overline{CD}[/tex] uma altura deste triângulo, prove que os ângulos [tex]D\hat{C}E~[/tex] e [tex]~E\hat{C}F[/tex] têm a mesma medida.

Lembretes
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
(2) Todo triângulo isósceles possui os ângulos da base com mesma medida.
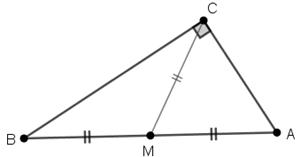
(3) A mediana de um triângulo retângulo relativa à hipotenusa mede metade da hipotenusa.
Solução
Considere [tex]x[/tex] e [tex]y[/tex] as medidas, em graus, dos ângulos [tex]B \hat{A}C[/tex] e [tex]C \hat{B}A[/tex], respectivamente.
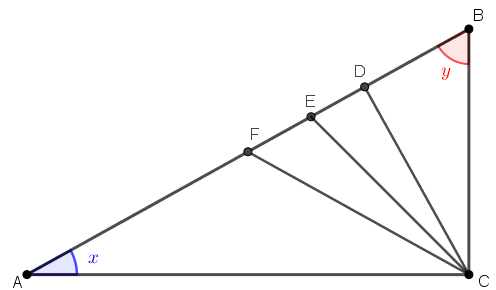
Como [tex]A \hat{C}B[/tex] é um ângulo reto, temos que [tex]x[/tex] e [tex]y[/tex] são medidas de ângulos complementares ([tex]x+y=90^\circ[/tex]).
Além disso, [tex]B \hat{D}C[/tex] é reto, sendo [tex]B \hat{C}D[/tex] complemento de [tex]D \hat{B}C[/tex]; logo, a medida do ângulo [tex]B \hat{C}D[/tex] é também [tex]x[/tex].
Sabemos que em um triângulo retângulo a mediana relativa à hipotenusa mede metade desta; assim, os segmentos [tex]\overline{AF}~[/tex] e [tex]~\overline {FC}[/tex] têm mesma medida. Portanto, o triângulo [tex]AFC[/tex] é isósceles e, consequentemente, os ângulos [tex]F \hat{A}C[/tex] e [tex]F \hat{C}A[/tex] são congruentes e têm medida [tex]x[/tex].
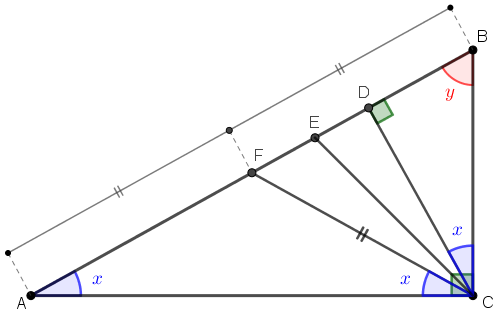
Se [tex]\overline{CE}[/tex] é bissetriz de [tex]B \hat{C}A[/tex], que é um ângulo reto, então a medida dos ângulos [tex]A \hat{C}E~[/tex] e [tex]~B \hat{C}E[/tex] é [tex]45^\circ[/tex].
Finalmente, temos que os ângulos [tex]E \hat{C}F[/tex] e [tex]D \hat{C}E[/tex] são congruentes com medidas iguais a [tex]~\boxed{45^\circ-x~}.[/tex]
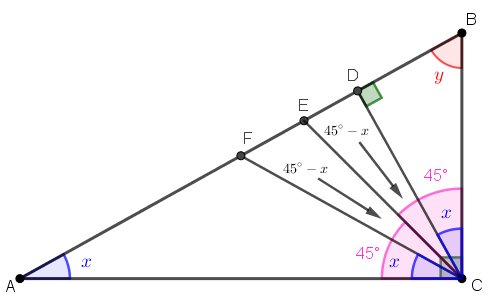
Solução elaborada pelos Moderadores do Blog.
