.Problemão: Encontre as medidas dos ângulos

Problema
(Indicado a partir do 9º ano do E. F.)

(Extraído da X-OMR) Seja [tex]ABC[/tex] um triângulo equilátero de baricentro [tex] O[/tex] e lado medindo [tex] 3[/tex]. Considere [tex] P[/tex] um ponto sobre o lado [tex]\overline{AB}[/tex] tal que [tex]AP=1[/tex] e [tex]M[/tex] sobre o lado [tex]\overline{AC}[/tex] tal que [tex]CM=1[/tex].
Encontre as medidas dos ângulos do triângulo [tex]MOP[/tex].

explicador_p

Lembretes e notações

[tex]\textcolor{#800000}{\textbf{(i)}}\; \textbf{ (Lei dos Cossenos)}[/tex] Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\quad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\quad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\quad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
[tex]\textcolor{#800000}{\textbf{(ii)}}\;[/tex] Em um triângulo equilátero [tex]ABC[/tex] de lado [tex]l[/tex], qualquer uma das três alturas mede [tex]\dfrac{l\sqrt{3}}{2}[/tex].
[tex]\textcolor{#800000}{\textbf{(iii)}}\;[/tex] Em um triângulo equilátero [tex]ABC[/tex], o baricentro (que também é incentro, circuncentro e ortocentro) divide os segmentos relativos às alturas (que também são medianas, mediatrizes e bissetrizes) numa razão de [tex]2[/tex] para [tex]1[/tex].
[tex]\textcolor{#800000}{\textbf{(iv)}}\;[/tex] A soma das medidas dos ângulos internos de qualquer triângulo vale [tex]180^{\circ}[/tex].
Notações: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].

Solução

De acordo com o problema considere o triângulo equilátero [tex]ABC[/tex] e o triângulo [tex]MOP[/tex], como na figura.

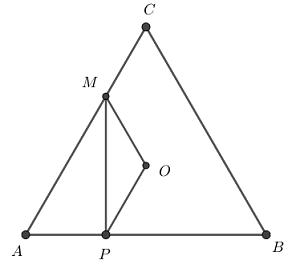
Notemos que [tex]AC=AB=BC=3[/tex], [tex]MC=1=AP[/tex] e [tex]AM=2[/tex].
Considere [tex]Q[/tex] o ponto médio do lado [tex]\overline{AB}[/tex]. Logo, [tex]\overline{CQ}[/tex] é altura (mediana e mediatriz) em relação ao lado [tex]\overline{AB}[/tex] e, como [tex]O[/tex] é o baricentro do triângulo equilátero [tex]ABC[/tex], então [tex]O\in \overline{CQ}[/tex].

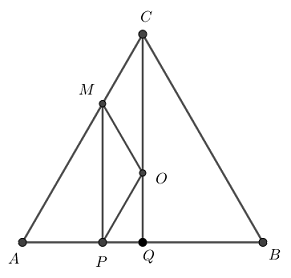
  • No triângulo [tex]APM[/tex] temos [tex]\widehat{MAP}=60^{\circ}[/tex], [tex]AM=2[/tex] e [tex]AP=1[/tex]; então, aplicando o [tex]\textcolor{#800000}{\textbf{Lembrete (i)}}[/tex], segue que:

    • [tex]\qquad (MP)^2=(AM)^2+(AP)^2-2\cdot (AM)\cdot (AP)\cdot \cos 60^{\circ}[/tex]
    [tex]\qquad (MP)^2=(2)^2+(1)^2-2\cdot 2\cdot 1\cdot \dfrac{1}{2}[/tex]
    [tex]\qquad (MP)^2=4+1-2[/tex]
    [tex]\qquad (MP)^2=3[/tex]
    [tex]\qquad MP=\pm \sqrt{3}[/tex].
    Como [tex]MP[/tex] é um comprimento, [tex]\boxed{MP=\sqrt{3}}[/tex].

  • Do [tex]\textcolor{#800000}{\textbf{Lembrete (ii)}}[/tex] temos que [tex]CQ=\dfrac{3\sqrt{3}}{2}[/tex]; do [tex]\textcolor{#800000}{\textbf{Lembrete (iii)}}[/tex] temos [tex]CO=\dfrac{2}{3}\cdot \dfrac{3\sqrt{3}}{2}=\sqrt{3}[/tex] e [tex]OQ=\dfrac{1}{3}\cdot\dfrac{3\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}[/tex].

    • Por outro lado, notemos que o triângulo [tex]OQP[/tex] é retângulo, [tex]PQ=\dfrac{1}{2}[/tex] e [tex]OQ=\dfrac{\sqrt{3}}{2}[/tex]; assim, aplicando o Teorema de Pitágoras, segue que:
    [tex]\qquad (OP)^2=(PQ)^2+(OQ)^2[/tex]
    [tex]\qquad (OP)^2=\bigg(\dfrac{1}{2}\bigg)^2+\bigg(\dfrac{\sqrt{3}}{2}\bigg)^2[/tex]
    [tex]\qquad (OP)^2=\dfrac{1}{4}+\dfrac{3}{4}[/tex]
    [tex]\qquad (OP)^2=1[/tex]
    [tex]\qquad OP=\pm 1[/tex].
    Sendo [tex]OP[/tex] um comprimento, [tex]\boxed{OP=1}[/tex].

  • No triângulo [tex]CMO[/tex] temos que [tex]OC=\sqrt{3}[/tex], [tex]CM=1[/tex] e [tex]\widehat{MCO}=30^{\circ}[/tex](já que [tex] \widehat{ACB}=60^{\circ}[/tex] e [tex]\overline{CO}[/tex] é bissetriz de [tex]\widehat{ACB}[/tex]). Assim, pelo [tex]\textcolor{#800000}{\textbf{Lembrete (i)}}[/tex]:

    • [tex]\qquad (MO)^2=(OC)^2+(CM)^2-2\cdot (OC)\cdot (CM)\cdot \cos 30^{\circ}[/tex]
    [tex]\qquad (MO)^2=(\sqrt{3})^2+1^2-2\cdot \sqrt{3}\cdot 1\cdot \dfrac{\sqrt{3}}{2}[/tex]
    [tex]\qquad (MO)^2=3+1-3[/tex]
    [tex]\qquad (MO)^2=1[/tex]
    [tex]\qquad MO=\pm 1[/tex], ou seja, [tex]\boxed{MO=1}[/tex].

  • No triângulo [tex]MOP[/tex] obtemos que [tex]MP=\sqrt{3}[/tex], [tex]OP=1[/tex] e [tex]OM=1[/tex], ou seja, [tex]MOP[/tex] é um triângulo isósceles de base [tex]\overline{PM}[/tex]. Vamos calcular [tex]\widehat{MOP}[/tex], utilizando o [tex]\textcolor{#800000}{\textbf{Lembrete (i)}}[/tex]:

    • [tex]\qquad (MP)^2=(OM)^2+(OP)^2-2\cdot (OM)\cdot (OP)\cdot \cos \widehat{MOP}[/tex]
    [tex]\qquad (\sqrt{3})^2=1^2+1^2-2\cdot 1\cdot 1\cdot \cos \widehat{MOP}[/tex]
    [tex]\qquad 3=2-2 \cos \widehat{MOP}[/tex]
    [tex]\qquad \cos \widehat{MOP}=-\dfrac{1}{2}[/tex],
    donde, [tex]\boxed{ \widehat{MOP}=120^{\circ}}[/tex].

Finalmente, pelo [tex]\textcolor{#800000}{\textbf{Lembrete (iv)}}[/tex] e considerando [tex]\widehat{OPM}=\widehat{OMP}=\alpha[/tex], temos:
[tex]\qquad 120^{\circ}+\alpha +\alpha=180^{\circ}[/tex]
[tex]\qquad 2\alpha=60^{\circ}[/tex]
[tex]\qquad \alpha=30^{\circ}[/tex].
Portanto, [tex]\,\fcolorbox{black}{#eee0e5}{$\widehat{OPM}=\widehat{OMP}=30^{\circ}$}[/tex] e [tex]\,\fcolorbox{black}{#eee0e5}{$\widehat{POM}=120^{\circ}$}\,.[/tex]

Solução elaborada pelos Moderadores do Blog.

Link permanente para este artigo: http://clubes.obmep.org.br/blog/problemao-encontre-as-medidas-dos-angulos/