Problema
(Indicado a partir do 9º ano do E. F.)
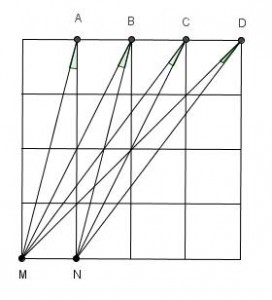
Na figura temos um quadrado dividido em 16 quadrados congruentes.
Determine, em graus, a seguinte soma de ângulos: [tex]M\hat{A}N+M\hat{B}N+M\hat{C}N+M\hat{D}N[/tex].
Solução
Na resolução do problema, utilizaremos duas proposições:
(1) Se dois segmentos são congruentes e paralelos, então suas extremidades são vértices de um paralelogramo.
(2) Se os lados de um ângulo são paralelos aos lados de outro ângulo, então estes ângulos são congruentes ou suplementares.
Observe a figura abaixo.
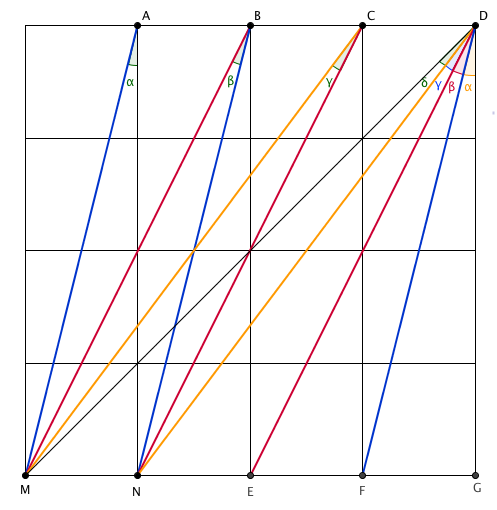
Por (1), podemos garantir que os segmentos de mesma cor são paralelos (e também são congruentes). Por exemplo, os segmentos [tex]AB[/tex] e [tex]MN[/tex] são paralelos e congruentes, logo [tex]AMNB[/tex] é um paralelogramo, de onde se conclui que [tex]AM[/tex] e [tex]BN[/tex] são paralelos.
Note, também, que os ângulos em destaque na figura são todos agudos; portanto, por (2), temos que:
[tex]\qquad \bullet M \hat{D}E = M \hat{C}N = \gamma[/tex]
[tex]\qquad \bullet E \hat{D}F = M \hat{B}N = \beta[/tex]
[tex]\qquad \bullet M \hat{A}N = F \hat{D}G = \alpha[/tex].
Veja que, pelas hipóteses, [tex]\Delta MDG[/tex] é retângulo e isósceles (observe que a figura inicial é um quadrado), tendo assim ângulos agudos de [tex]45^{\circ}.[/tex]
Assim,
[tex]\qquad M\hat{A}N+M\hat{B}N+M\hat{C}N+M\hat{D}N=\alpha + \beta + \gamma + \delta = 45^\circ[/tex].
Você saberia justificar as duas proposições utilizadas na resolução deste problema?
Solução elaborada pelos Moderadores do Blog.
