Problema
(Indicado a partir do 9º ano do E. F.)
(Canguru, 2014-Adaptado) O quadrado [tex]XYZW[/tex] tem os vértices [tex]X[/tex] e [tex]Y[/tex] sobre a reta [tex]r[/tex] e os vértices [tex]Z[/tex] e [tex]W[/tex] sobre as circunferências de centros [tex]O[/tex] e [tex]O'[/tex], sendo essas circunferências, de raios medindo [tex]2\;cm[/tex], tangentes entre si e à reta [tex]r[/tex], como na figura abaixo.
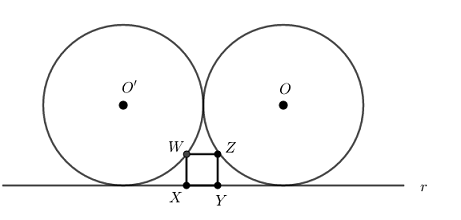
Encontre a medida do lado do quadrado [tex]XYZW[/tex].

Lembretes e notação
[tex]\textcolor{#800000}{(1)}[/tex] Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
[tex]\textcolor{#800000}{(2)}[/tex] As raízes da equação do segundo grau [tex]~~ax^2+bx+c = 0~~[/tex] são dadas por
[tex]~~~~~~~~~~~~x_1 = \dfrac{-b+\sqrt{\Delta}}{2a}~~~[/tex] e [tex]~~~x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}[/tex],
onde [tex]a,b,c[/tex] são números reais, com [tex]a\ne 0~[/tex], e [tex]~\Delta =b^2-4ac[/tex].
Notação:
– Denotaremos o comprimento do segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]XY[/tex].
Solução
A partir dos dados do problema, considere [tex]A[/tex] o ponto de tangência entre as circunferências e [tex]B[/tex] o ponto de tangência da circunferência de centro [tex]O[/tex] com a reta [tex]r[/tex]. Como o raio de cada circunferência mede [tex]2\;cm[/tex] temos que [tex]AO=OB=2[/tex]. Considere a reta [tex]s[/tex] perpendicular à reta [tex]r[/tex] e passando pelo ponto [tex]A[/tex]. Pela simetria da figura, notemos que a interseção das retas [tex]r[/tex] e [tex]s[/tex] é o ponto médio, [tex]M[/tex], do lado do quadrado que está sobre a reta [tex]r[/tex]. Assim, [tex]AO=MB=2[/tex].
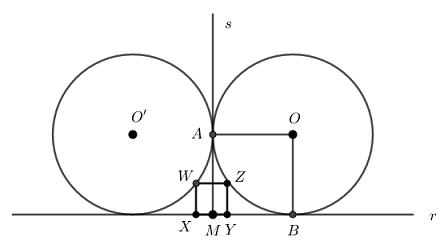
Seja [tex]l[/tex] o lado do quadrado [tex]XYZW[/tex] e considere o triângulo retângulo [tex]ZPO[/tex], como na figura abaixo.
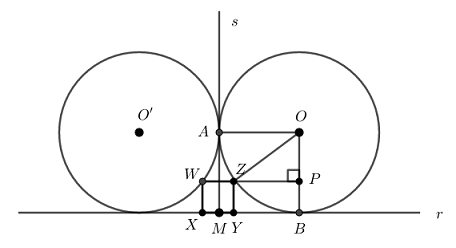
Observe que
- [tex]ZP=YB=MB-\dfrac{l}{2}=2-\dfrac{l}{2}[/tex],
- [tex]OZ=2[/tex],
- [tex]OP=2-l[/tex],
assim, aplicando o Teorema de Pitágoras no triângulo [tex]ZPO[/tex] segue que:
[tex]\qquad (OZ)^2= (ZP)^2+(OP)^2\\
\qquad 2^2=\bigg(2-\dfrac{l}{2}\bigg)^2+(2-l)^2\\
\qquad 4=4-2l+\dfrac{l^2}{4}+4-4l+l^2\\
\qquad 5l^2-24l+16=0.\qquad \textcolor{#800000}{(i)}[/tex]
Vamos, então, resolver a equação [tex]\textcolor{#800000}{(i)}[/tex]:
[tex]\qquad l=\dfrac{24\pm\sqrt{576-320}}{10}\\
\qquad l=\dfrac{24\pm\sqrt{256}}{10}\\
\qquad l=\dfrac{24\pm 16}{10}[/tex]
[tex]\qquad l=4[/tex] ou [tex]l=\dfrac{4}{5}\,.[/tex]
Como o lado do quadrado [tex]XYZW[/tex] não é maior do que os raios das circunferências, temos que o comprimento do lado desse quadrado é [tex]\,\fcolorbox{black}{#eee0e5}{$l=\dfrac{4}{5}\text{ cm }$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
